301CRS Algebra 3

CMI, Aug-Nov 2025, Clare D’Cruz
Artin (2011), Dummit & Foote (2004), Aluffi (2009) (Errata), Lang (2002), Hungerford (1974), Conrad’s expository papers, Authors (n.d.)

---

Intro to Category Theory
Intro to Ring Theory
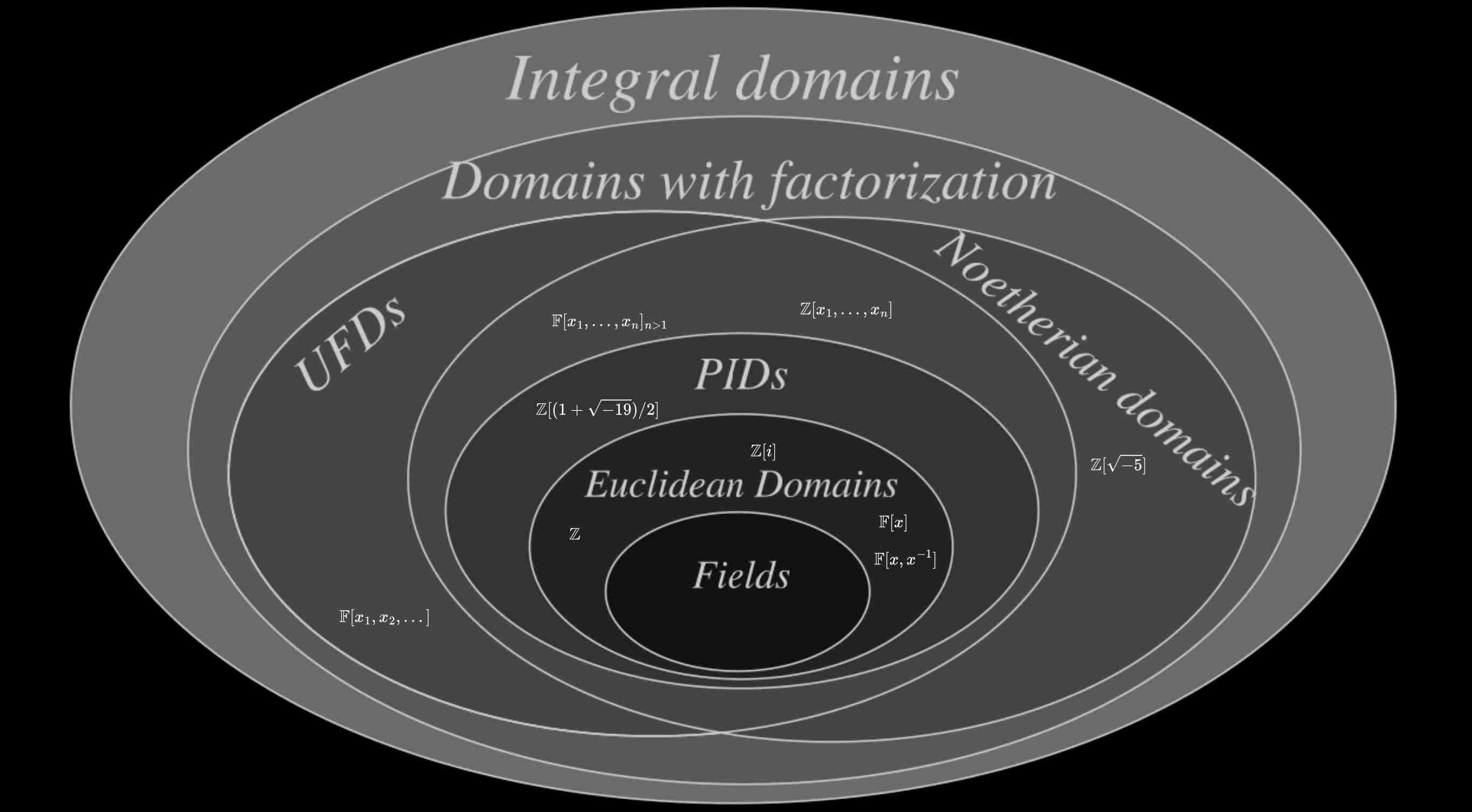
Quadratic integer rings

Lectures

LEC ALG3 1 ✅ Ring homomorphisms, polynomial rings, products and coproducts
LEC ALG3 2 ✅ Quotients and ideals
LEC ALG3 3 ✅ Modules
LEC ALG3 4 ✅ Quotients of polynomial rings, prime and maximal ideals, power series rings
LEC ALG3 5 ✅ Radicals
LEC ALG3 6 ✅ Krull’s theorem, Chinese remainder theorem
LEC ALG3 7 ✅ Irreducible and prime elements
LEC ALG3 8 ✅ Ring of fractions
LEC ALG3 9 ✅ Euclidean domains and unique factorization domains
LEC ALG3 10 ✅ Gauss’s Lemma, $R$ is UFD $⟹$ $R[x]$ is UFD
LEC ALG3 11 Gaussian primes
LEC ALG3 12 More on factoring
LEC ALG3 13 Eisenstein’s Criterion
LEC ALG3 15 ✅ Algebraic elements and algebraic extensions
LEC ALG3 16 ✅ Towers of algebraic extensions
LEC ALG3 17 ✅ Algebraic elements form a subextension
LEC ALG3 19 ✅ Algebraic closure
LEC ALG3 20 ✅ Splitting fields, gcd
LEC ALG3 21 ✅ Finite fields

🎉

Tutorials

TUT ALG3 1
TUT ALG3 2
TUT ALG3 3
TUT ALG3 4
TUT ALG3 5
TUT ALG3 6
TUT ALG3 7
TUT ALG3 8
TUT ALG3 9

TST ALG3 Midsem
TST ALG3 Quiz2

---

References

Aluffi, P. (2009). Algebra: Chapter 0. American Mathematical Society.

Artin, M. (2011). Algebra (2. ed). Pearson Education, Prentice Hall.

Authors, T. S. P. (n.d.). Fields. Retrieved November 17, 2025, from https://stacks.math.columbia.edu/tag/09FA

Dummit, D. S., & Foote, R. M. (2004). Abstract Algebra (3rd ed). Wiley.

Hungerford, T. W. (1974). Algebra (Vol. 73). Springer New York. https://doi.org/10.1007/978-1-4612-6101-8

Lang, S. (2002). Algebra (Vol. 211). Springer New York. https://doi.org/10.1007/978-1-4613-0041-0