DMAT_L2

Sets

Cantor diagonalization: Reals are not countable.
Sets $A$ and $B$ are said to have the same cardinality if there exists a bijection between them.

Cardinal arithmetic

Let $|A|=\alpha$ and $|B|=\beta$. $\alpha$ and $\beta$ are called cardinal numbers.
Assume $A$ and $B$ are disjoint.

Defining cardinal arithmetic

• $\alpha +\beta =|A\bigsqcup B|$.
• $\alpha \beta =|A\times B|$.
• ${\alpha }^{\beta }=|A^B|=\{\text{set of all functions from B to A}\}$.

Things to verify

• $(\alpha +\beta )\gamma =\alpha \gamma +\beta \gamma$.
  • Let $|A|=\alpha$, $|B|=\beta$, $|C|=\gamma$.
  • $(\alpha +\beta )\gamma =|(A\cup B)\times C|$.
  • $\alpha \gamma +\beta \gamma =|A\times C\cup B\times C|$.
  • we need to supply a bijection between the two sets, which is just the identity map.
• $\alpha \beta =\beta \alpha$
  • $(a,b)\mapsto (b,a)$
• $({\alpha }^{\beta }{)}^{\gamma }={\alpha }^{\beta \gamma }$
  • We need to construct a bijection $\varphi :(A^B{)}^C\to A^{B\times C}$.
  • define $\varphi (f)$ to be $g$ where $g(b,c)=f(c)(b)$.
  • $(A^B{)}^C$ is a set of functions which take in an element from $C$ and give a function which maps from $B$ to $A$. Similar to how currying works in functional programming languages.
• ${\alpha }^{\beta +\gamma }={\alpha }^b{\alpha }^{\gamma }$
  • We need a bijection between $A^{B\cup C}$ and $A^B\times A^C$.
  • Define $\varphi :A^{B\cup C}\to A^B\times A^C$ such that $\varphi (f)=(f{|}_B,f{|}_A)$, where $f{|}_B$ and $f{|}_A$ are the restrictions of $f$ to $B$ and $A$ respectively.

Comparing cardinalities

For two sets $A$ and $B$, we say that $|A|\le |B|$ if there is an injective map $\varphi :A\to B$ (or, equivalently, if there exists a surjective map $\psi :B\to A$).

Theorem 1(Lemma).

Let $A$, $B\ne \varnothing$. There exists an injection from $A$ to $B$ iff there exists a surjection from $B$ to $A$.

Proof of $⟹$
$\varphi :A\to B$, injective.
Want $\psi :B\to A$, surjective.

$$\psi (b)\equiv \{\begin{array}{ll}x& f(x)=b\\ a& \nexists \text{ such an }x\end{array}$$

for some $a\in A$.

Proof of $⟸$
$\psi :B\to A$, surjective.

$\varphi (a)\equiv \text{ some }b\in {\psi }^{-1}(a)$. (This requires the axiom of choice)

$|A|<|B|$ if there exists an injection from $A$ to $B$ but no bijection. (requires AOC)

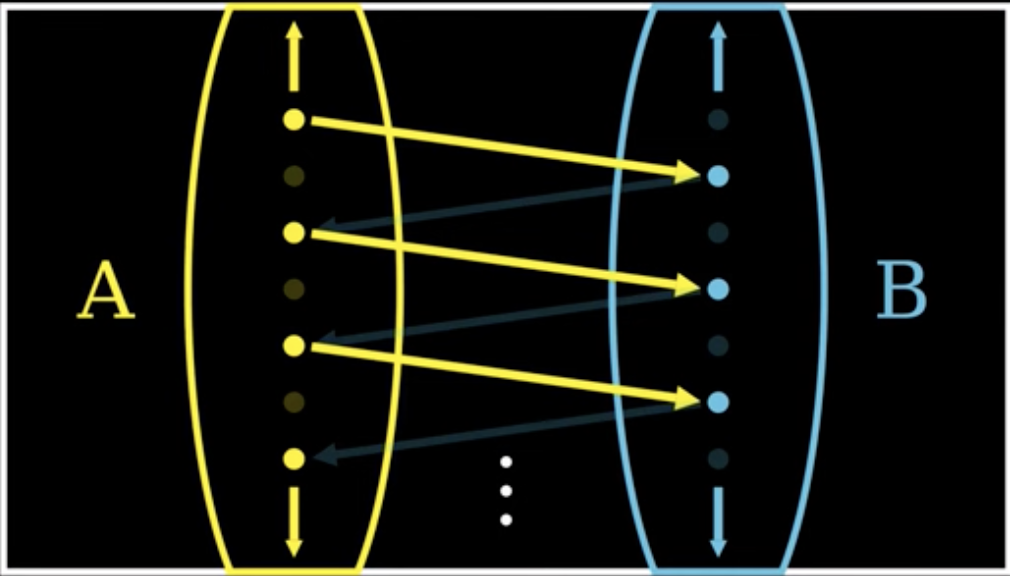
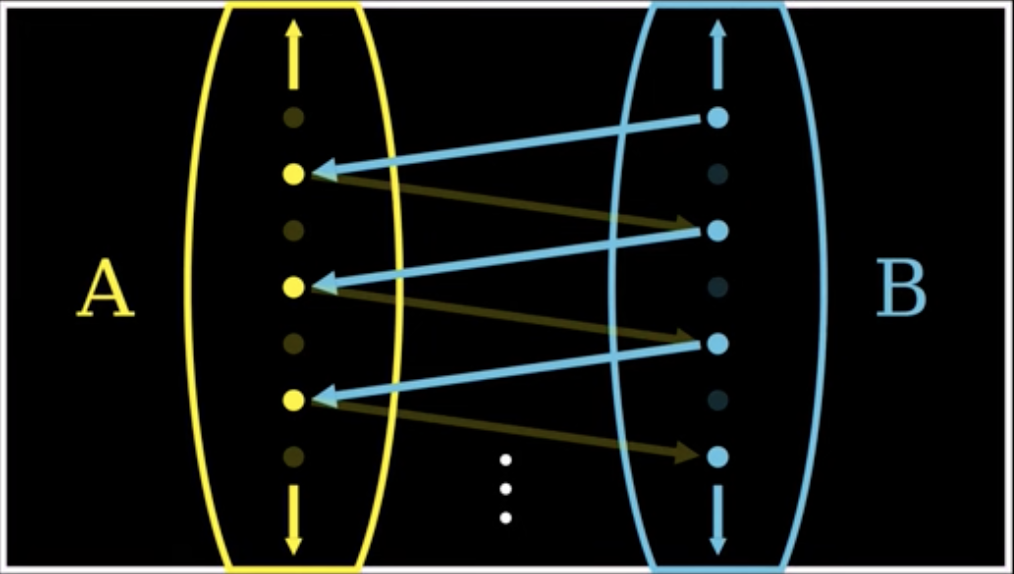
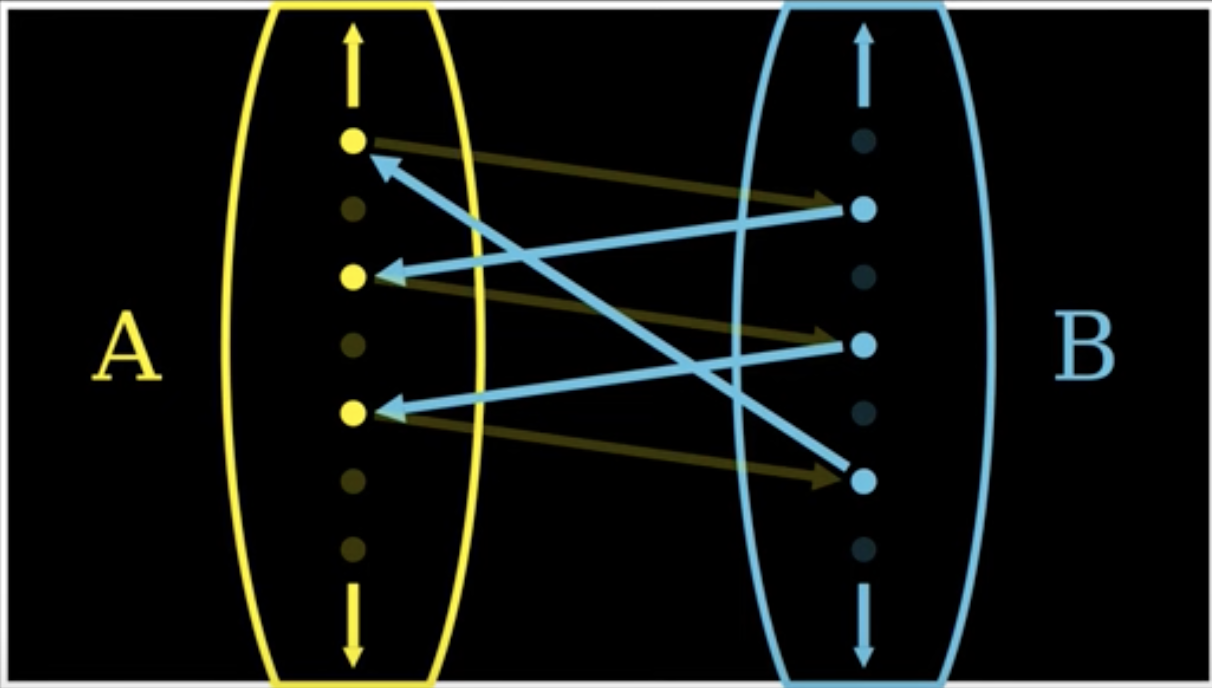
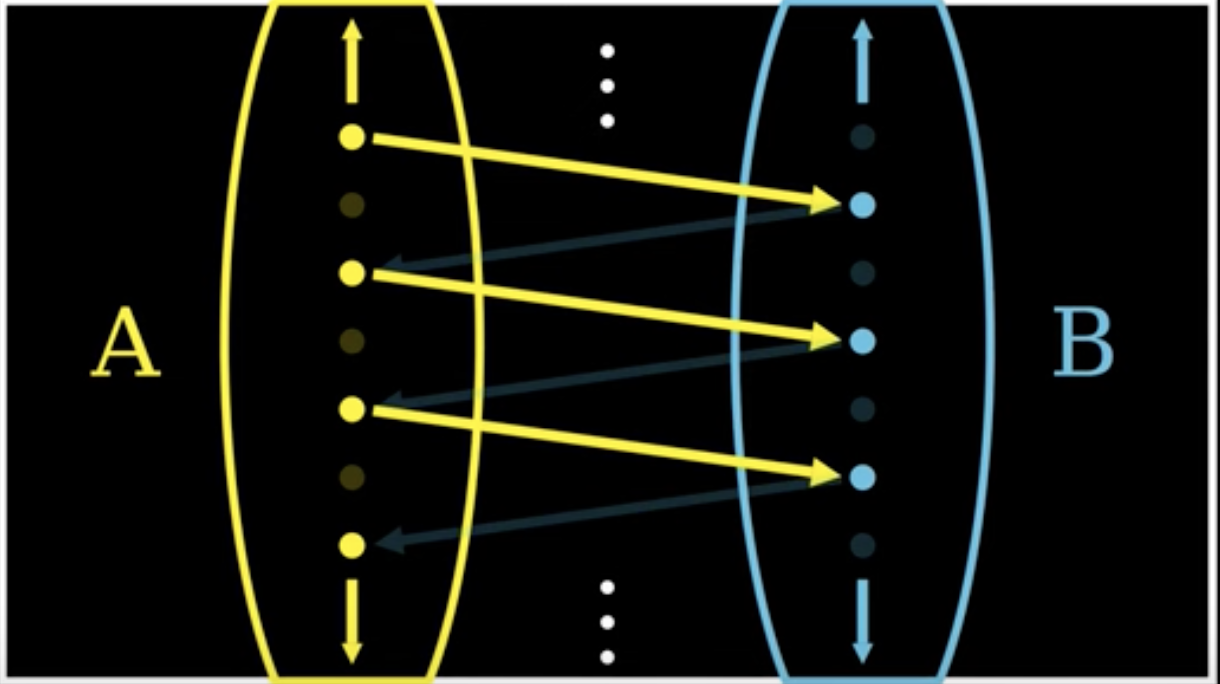
Schröder–Bernstein theorem

Theorem 2(Schroder-Bernstein Theorem).

If $f:A\to B$ is an injection and $g:B\to A$ is a injection, then $|A|=|B|$.

Makes proving things like $|\mathbb{N}\times \mathbb{N}|=|\mathbb{N}|$ easy.

Proof 1
Assume $A$ and $B$ are disjoint so the notation does not become too cumbersome.
Consider the set of all sequences $S=\{(\dots ,f^{-1}(g^{-1}(a)),g^{-1}(a),a,f(a),g(f(a)),f(f(g(a))),\dots ):a\in A\}$. If $a$ does not have a preimage under $g$, the sequence starts at $a$ (Note the set of sequences obtained by $b\in B$ and interchanging $f$ and $g$ is equal to $S$). So, every element $e\in A\cup B$ appears in one (and exactly one) sequence in $S$. The a sequence $s$ in $S$ can be characterized like so:

• Starts at $A$: Has a first element in $A$ which does not have a preimage under $g$. Denoted by $s\in S_A$.
  
• Starts at $B$: Has a first element in $B$ which does not have a preimage under $f$. Denoted by $s\in S_B$.
  
• Loops forever: Continues forever in both directions, but the elements loop. $s\in S_l$
  
• Continues forever in both directions, but does not loop. $s\in S_{\infty }$
  

Note that sequences in $S_A$ and $S_B$ are incapable of looping. Thus, $S_A$, $S_B$, $S_l$, and $S_{\infty }$ actually form a partition of $S$.

Now, if $s\in S_A$, note that $f$ is surjective when its domain is restricted to $s\cap A$ and codomain is restricted to $s\cap B$. Similarly, if $s\in S_B$, $g$ is surjective when its domain is restricted to $s\cap B$ and codomain is restricted to $s\cap A$ (or, equivalently, $g^{-1}$ is surjective with its domain restricted to $s\cap A$ and codomain restricted to $s\cap B$). Note that since these functions were already known to be injective, surjectivity makes them bijective.

Finally, note that both $f$ and $g$ are bijective for sequences in $S_l$ and $S_{\infty }$, when their domains and codomains are restricted appropriately.

Thus, it makes sense to construct a function $h:A\to B$:

$$h(a)\equiv \{\begin{array}{ll}f(a)& a\in s,s\in S_A\cup S_l\cup S_{\infty }\\ g^{-1}(a)& a\in s,s\in S_B.\end{array}$$

It is easy to see that $h$ is a bijection. ◻️

Proof 2 (Done is class, essentially the same idea as the previous one)
For each $a\in A$, the parent of $a$ is $g^{-1}(a)$, if it exists. Ditto for each $b\in B$.
For each $a\in A$, we get a sequence $(a_0,a_1,\dots ,a_n)$ ending at $a_n$ or going off to infinity, where $a_i$ is the parent of $a_{i-1}$. Now, the chain can be of

• infinite length (in which case we say $a\in A_{\infty }$),
• even length(length = $n$), or ends at $A$ ($a\in A_e$),
• odd length, or ends at $B$ ($a\in A_o$).

So, we get a partition $A=A_{\infty }\bigsqcup A_l\bigsqcup A_o$.
Ditto for $B$.

Note that $f$ maps $A_e$ to $B_o$, and $g$ maps $B_e$ to $A_o$. Also note that the restrictions of $f$ and $g$ to $A_e$ and $B_e$ respectively (with their codomains restricted to $B_o$ and $A_o$ respectively) are surjective. Hence, these restrictions are bijective.
Also note that $f$ and $g$ map bijectively between $A_{\infty }$ and $B_{\infty }$.

Define $h:A\to B$ by

$$h(x)\equiv \{\begin{array}{ll}f(x)& x\in A_e\cup A_{\infty }\\ g^{-1}(x)& x\in A_o\end{array}$$

$h$ is a bijection.

We can use the SBT to prove $|[0,1]\times [0,1]\times [0,1]|=|[0,1]|$: just interweave decimal representations for the injection from the cube to the line.
is it possible to define a continuous injective map from the cube to the line?

Theorem 3(Theorem).

For all $A,B$ either $|A|<|B|$, $|A|>|B|$, or $|A|=|B|$.

---

References:

• https://www.youtube.com/watch?v=Nv90aDcwzv0