DMAT_L14

Counting with Symmetries

We want to count the number of distinct  $r$-colorings of an object. Let $X$ be the set of elements being colored (e.g., faces or vertices). A coloring is a function $c:V\to [r]$. Two colorings are considered the same if one can be transformed into the other by applying a symmetry of the object, such as a rotation.

The symmetric group on $X$, denoted $\text{Sym}(X)$, consists of all possible permutations of $X$. However, not all elements of $\text{Sym}(X)$ correspond to physically realisable transformations of the object. Typically, we restrict our attention to a subgroup $G$ of rigid transformations, such as rotations. More generally, any subgroup of $\text{Sym}(X)$ can be considered, depending on the context.

Example 1(Equilateral Triangle).

Consider an equilateral triangle and a colour set of $\{R,B\}$. We wish to colour the vertices here, so $X$ will be the vertex set $\{1,2,3\}$. $\text{Sym}(X)\cong S_3$. Whether we take $G\cong S_3$ (flipping is allowed) or $G\cong C_3$ (can’t flip the triangle) doesn’t make a difference when we are working with only two colours. The possible colourings and transformations between them are as follows:

$$\begin{array}{rl}& RRR\\ & RRB\stackrel{(123)}{⟶}RBR\stackrel{(123)}{⟶}BRR\stackrel{(123)}{⟶}RRB\\ & BBR\stackrel{(123)}{⟶}RBB\stackrel{(123)}{⟶}BRB\stackrel{(123)}{⟶}RRB\\ & BBB\end{array}$$

There are four equivalence classes. Hence, there are four distinct ways of colouring the triangle.

Formalization using Group Actions

Let $X$ be a finite set that is to be coloured with $r$ colours. Let $G⩽\text{Sym}(X)$ be a finite group acting on $X$.

Notation

Let $G$ be a group acting on a set $X$. The group action of $g\in G$ on $x\in X$ is written as $x^g$. We follow multiplication from the left, so $x^{g_1{g}_2}=(x^{g_1}{)}^{g_2}$.

For some $\pi \in G$ and $x\in X$, define $x^{\pi }=\pi (x)$. It is easy to see that this will indeed be a group action.

Denote the set of all $r$-colourings $c:X\to [r]$ of $X$ by $\mathbb{C}$. Now let $G$ act on $\mathbb{C}$ as follows: for some $\pi \in G$ and $c\in \mathbb{C}$,

$$c^{\pi }=c^{\prime }\text{such that}{c}^{\prime }(x)=c(x^{{\pi }^{-1}}).$$

(The inverse is technically required to make this a valid action, but is also easy to intuitively validate).

Proof that this is a group action

1. For any $c\in \mathbb{C}$, $c^1=c^{\prime }$ where $c^{\prime }\in \mathbb{C}$ and $c^{\prime }(x)=c(x^1)=c(x)$, that is $c^1=c$.
2. For any $c\in \mathbb{C}$ and ${\pi }_1,{\pi }_2\in G$, we have

$$c^{{\pi }_1}\equiv c^{\prime }\text{and}(c^{\prime }{)}^{{\pi }_2}\equiv c^{\prime \prime }$$

where $c^{\prime }(x)=c(x^{{\pi }_1^{-1}})$ and $c^{\prime \prime }(x)=c^{\prime }(x^{{\pi }_2^{-1}})$. Now

$$\begin{array}{rl}(c^{{\pi }_1}{)}^{{\pi }_2}(x)& =(c^{\prime }{)}^{{\pi }_2}(x)\\ & =c^{\prime \prime }(x)\\ & =c^{\prime }(x^{{\pi }_2^{-1}})\\ & =c((x^{{\pi }_2^{-1}}{)}^{{\pi }_1^{-1}})\\ & =c(x^{({\pi }_1{\pi }_2{)}^{-1}})\\ & =c^{{\pi }_1{\pi }_2}(x).\end{array}$$

Orbits

Recall that the action of $G$ defines an equivalence relation on $X$ as

$$x_1\sim x_2⟺x_2=x_1^g\text{for some g∈G}.$$

The equivalence classes so formed are the Orbit. Furthermore,

$$\begin{array}{rl}\mathcal{O}(x)& =\{y\in X|y=x^g,g\in G\},\\ G_x& =\{g\in G|x^g=x\}.\end{array}$$

Note that counting the number of distinct colorings is equivalent to counting the number of orbits in the action of $G$ on $\mathbb{C}$.

From the Orbit-stabilizer theorem, we have

$$|G|=|\mathcal{O}(x)||G_x|$$

Proof.

Quick Intuitive Proof

We construct a bijection between the elements of $\mathcal{O}(x)$ and the left cosets of $G_x$ in X.
For every $\sigma \in G$ which maps $x\to y$, notice that $G_x\sigma$ maps $x\to y$. Clearly this is a bijection. As the cosets of $G_x$ partition $G$, we arrive at our result.□

For $g\in G$, define $\text{fix}(g)\equiv |\{x\in X|x^g=x\}|$. Note that $\text{fix}(1)=|X|$.

Burnside’s Lemma

Theorem 2(Burnside's Lemma).

For a group $G$ acting on a set $X$, the number of orbits is

$$\frac{1}{|G|}\sum _{g\in G}\text{fix}(g).$$

Proof
We prove this by double counting. Let $X=\{x_1,x_2,\dots ,x_m\}$ and $G=\{g_1,g_2,\dots g_n\}$. Make an $m\times n$ matrix $(M_{ij})$ as follows such that

$$M_{ij}=\{\begin{array}{ll}1& \text{if}{x}_i^{g_j}=x_i\\ 0& \text{otherwise.}\end{array}$$

The column-wise sum will be the sum, over $g_j$, of all the $x_i$ that are fixed by a given $g_j$, ie. it is the sum of $\text{fix}(g_j)$. Hence

$$\text{Column-wise Sum}=\sum _{g\in G}\text{fix}(g).$$

The row-wise sum will be the sum, over $x_i$, of all those $g_j$ that fix $x_i$, ie. the stabilizer of $x_i$. Hence

$$\text{Row-wise Sum}=\sum _{x\in X}|G_x|.$$

Since they both represent the total number of $1s$ in the matrix, they are the same. Let ${\mathcal{O}}_1,{\mathcal{O}}_2,\dots ,{\mathcal{O}}_l$ be the distinct orbits in $X$, now

$$\begin{array}{rl}\sum _{g\in G}\text{fix}(g)& =\sum _{x\in X}|G_x|\\ & =\sum _{x\in X}\frac{|G|}{|\mathcal{O}(x)|}\\ & =|G|\sum _{k=1}^l\sum _{x\in {\mathcal{O}}_k}\frac{1}{|\mathcal{O}(x)|}.\end{array}$$

The inner sum will be $1$ since the term $\frac{1}{|{\mathcal{O}}_k|}$ is being added ${\mathcal{O}}_k$ number of times. Hence the $RHS$ will be $|G|$ times the number of orbits. Rearranging, we get

$$\text{\#orbits}=\frac{1}{|G|}\sum _{g\in G}\text{fix}(g).$$

An example: 2-colorings of a cube

Consider a cube with faces $R,L,F,B,U,D$ which correspond to Right, Left, Front, Back, Up and Down respectively.

Let $G$ denote the set of all orientations of a cube obtained through rotations. The cardinality of $G$ will be $24$.

Proof.

There are $6$ choices for the front face and $4$ for the side one; these uniquely determine an orientation.
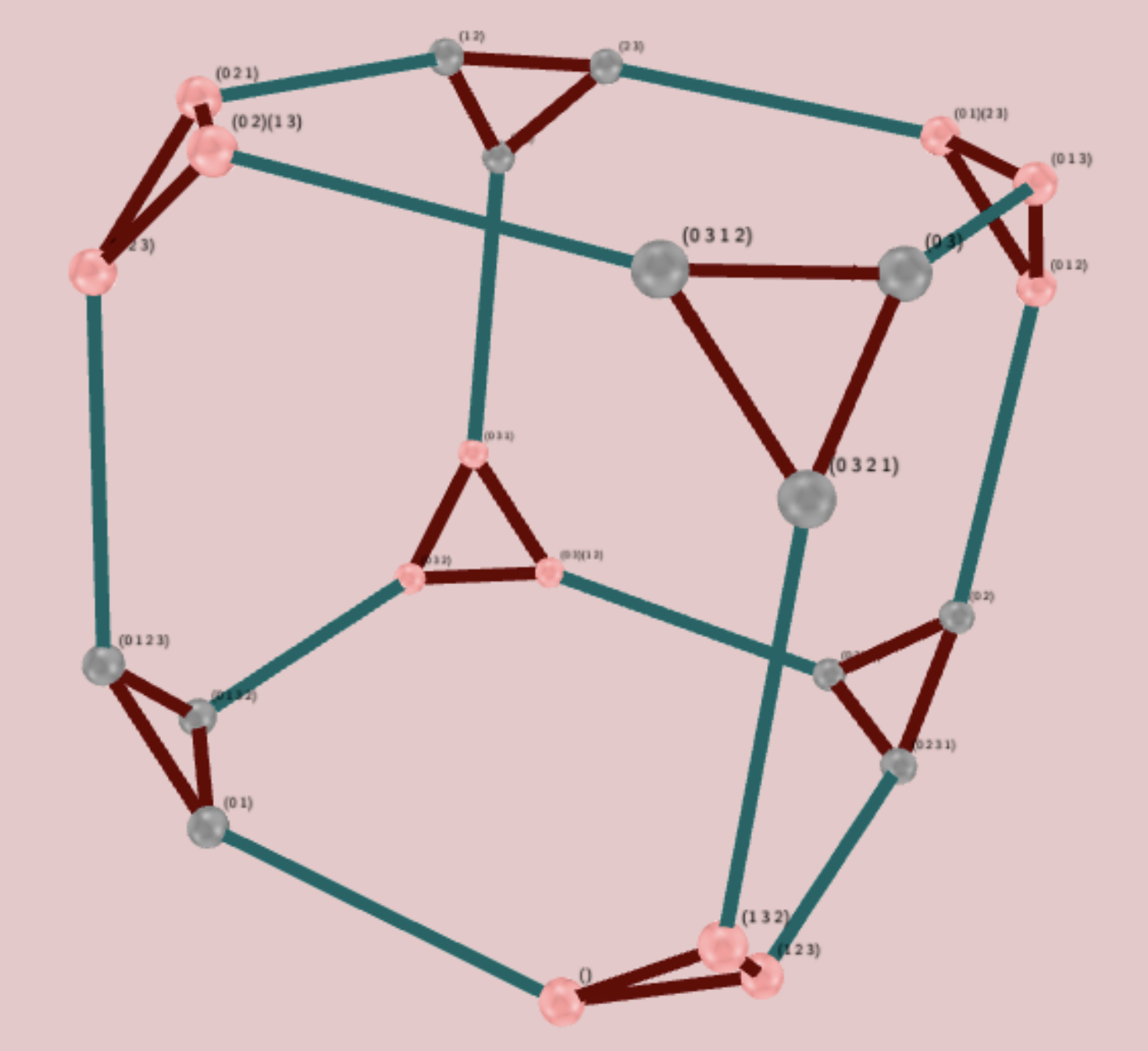
Alternatively, you can embed a tetrahedron in the cube such that its edges correspond with a set of pairwise non-adjacent edges of the cube (there are two such sets of edges). It will have two orientations upon rotating the cube. This will give a isomorphism to $S_4$.

The pink colored vertices form one tetrahedron, and the grey colored ones form another.□

There are four types of symmetries present here.

1. Face Symmetries ($180^{\circ }$ Rotations) - 3
   • $(U)(D)(FB)(RL)$
   • $(L)(R)(UD)(FB)$
   • $(F)(B)(RL)(UD)$
2. Face Symmetries ($90^{\circ }$ Rotations) - 6
   • $(U)(D)(FLBR)$ and its inverse
   • $(F)(B)(RDLU)$ and its inverse
   • $(R)(L)(UFDB)$ and its inverse
3. Edge Symmetries - 6
   • $(UD)(LB)(FR)$
   • $(UD)(LF)(BR)$
   • $(RL)(UF)(BD)$
   • $(RL)(FD)(UB)$
   • $(FB)(RU)(LD)$
   • $(FB)(RD)(LU)$
4. Vertex Symmetries - 8
   • $(FUR)(LBD)$ and its inverse
   • $(FRD)(UBL)$ and its inverse
   • $(RUB)(FLD)$ and its inverse
   • $(RDB)(FUL)$ and its inverse
5. The identity symmetry - 1
   • $(R)(L)(F)(B)(U)(D)$

All together, we have 24 symmetries, as expected. Note that for a symmetry $g$, $\text{fix}(g)=2^{{}^{c(g)}}$, where $c(g)$ is the number of cycles in the cycle representation of $g$. Using Burnside’s lemma,

$$\#\text{orbits}=\frac{1}{24}\left(3\times 2^4+6\times 2^3+6\times 2^3+8\times 2^2+1\times 2^6\right)=\frac{240}{24}=10.$$

Thus, there are $10$ distinct ways to 2-color a cube.

A note on the symmetries of a rigid solid