ALG2_L2

Symmetric groups

The set of all permutations of $(1,2,\dots ,n)$ form a group, denoted by $S_n$. A cycle is a special type of permutation. For example, $(12)$ is what is called a 2-cycle, and represents swapping $1$ and $2$. $(123)$ is a 3-cycle, and maps 1 to 2, 2 to 3, and 3 to 1. The group operation is composition. Starting from $S_3$, they are not abelian.

Theorem 1(Lemma).

Every $\tau \in S_n$ can be expressed as a product of cycles.

Proof
Let $i$ be the first element in $\{1,2,\dots ,n\}$ which is not fixed by $\tau$ (i.e, is not mapped to itself. Fixed elements form cycles of length 1). Consider the cycle ${\sigma }_1=(1\tau (1){\tau }^2(1)\dots )$. Repeat until you have exhausted all elements, at which point $\tau$ can be expressed as a product of disjoint cycles, $\tau ={\sigma }_1{\sigma }_2\dots {\sigma }_k$. Note that the cycles being disjoint makes their product commutative, i.e, we can write the product in any order.

Now, let the sign of a permutation be defined as the number of “disorders” in the permutation, as done here. Note with this definition, the sign of a permutation is a well defined quantity. It can easily be verified that if a cycle $\sigma$ has length $k$, $\text{sgn}(\sigma )=(-1{)}^{k-1}$. Thus, if $\tau ={\sigma }_1{\sigma }_2\dots {\sigma }_k$, $\text{sgn}(\tau )=\text{sgn}({\sigma }_1)\text{sgn}({\sigma }_2)\dots \text{sgn}({\sigma }_k)$.

Why is the sign of a permutation well defined, and why is the sign of a product equal to the product of the signs?

First, notice that the number of disorders of a permutation is a well defined number. Also notice that the number of disorders of the identity permutation is 0. Also notice that swapping two adjacent elements changes the number of disorders by $\pm 1$. Also notice that swapping any two elements using adjacent swaps takes an odd number of adjacent swaps, and thus changes the number of disorders by an odd number. Let the number of disorders of a permutation $\tau$ be $k$. If we start from the identity permutation and work our way towards $\tau$ by swapping any two elements at a time, notice that regardless of the path we take, the number of swaps we make MUST equal the parity of $k$. For example, if $k$ is odd, it is impossible to reach $\tau$ from the identity permutation by making an even number of swaps. Thus, we can safely say that the sign of a permutation is the number of swaps it takes us to get to it from the identity permutation.

Now, composing permutations. Let ${\tau }_1$ and ${\tau }_2$ be permutations with number of disorders $k_1$ and $k_2$ respectively. Composing them like ${\tau }_1\circ {\tau }_2$ entails applying ${\tau }_1$ first, then ${\tau }_2$ (using the convention that function composition is evaluated from the left, to stay consistent with Visual Group Theory). Now, the parity of the number of swaps to get to ${\tau }_1\circ {\tau }_2$ from $e$ is the product of (the parity of number of swaps to get to ${\tau }_1$ from $e$)$\times$ (the parity of the number of swaps to get to ${\tau }_1\circ {\tau }_2$ from ${\tau }_1$), with the latter being the same as the parity of the number of swaps to get to ${\tau }_2$ from $e$.

---

Homomorphisms

Definition 2(Definition).

Let $G=(G,\star )$ and $H=(H,\ast )$ be groups. A map $\varphi :G\to H$ is called an homomorphism if

$$\varphi (g_1\star g_2)=\varphi (g_1)\ast \varphi (g_2)\forall g_1,g_2\in G.$$

A homomorphism is basically a structure preserving map.

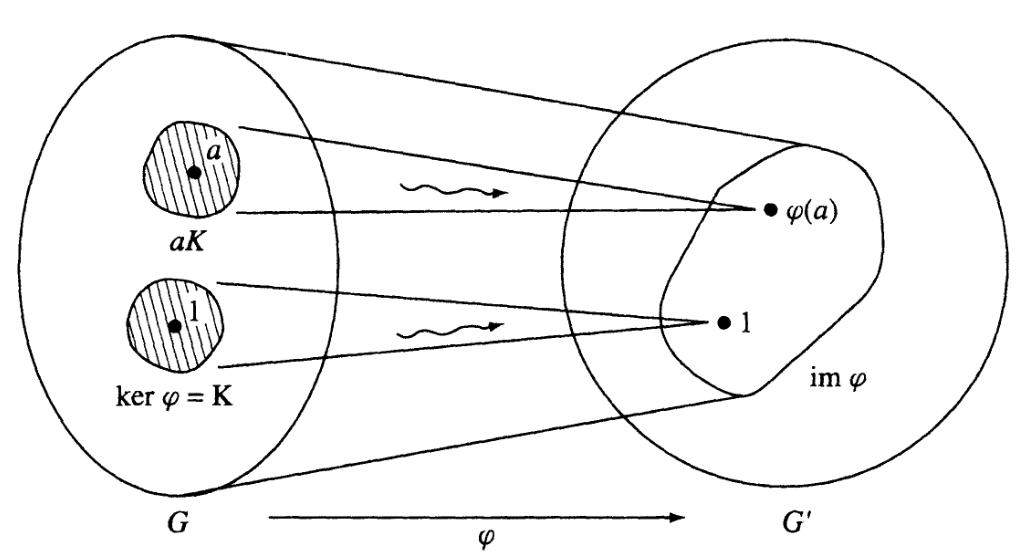
The kernel of $\varphi$ is the set of all elements in $G$ that it maps to the identity in $H$. The image of $\varphi$ is the set of all elements in $H$ that have a preimage in $G$.

Theorem 3(Properties of homomorphisms).

Let $\varphi$ be as defined above. For brevity, we will drop the $\star$ and $\ast$ symbols.

1. $\varphi$ will always map $1_G$ to $1_H$.
2. $\ker \varphi <G$.
3. $\mathrm{Im}\varphi <H$.

Proof of 1
$\varphi (1_G)=\varphi (1_G{1}_G)=\varphi (1_G)\varphi (1_G)$. It follows that $\varphi (1_G)=1_H$.

Proof of 2
Let $g_1,g_2\in \ker \varphi$. Then, $\varphi (g_1{g}_2)=\varphi (g_1)\varphi (g_2)=1_H{1}_H=1_H$. Thus, $g_1{g}_2\in G$. $\varphi (1_G)=1_H$, so $1_G\in \ker \varphi$. Also, $1_H=\varphi (1_G)=\varphi (g_1{g}_1^{-1})=\varphi (g_1)\varphi (g_1^{-1})=\varphi (g_1^{-1})$, i.e, $g_1^{-1}\in \ker \varphi$. Thus, $\ker \varphi <G$.

Proof of 3
Let $h_1,h_2\in \mathrm{Im}\varphi$. There must exist $g_1,g_2\in G$ such that $\varphi (g_1)=h_1$ and $\varphi (g_2)=h_2$. Then, $\varphi (g_1{g}_2)=\varphi (g_1)\varphi (g_2)=h_1{h}_2$. Thus, $h_1{h}_2\in \mathrm{Im}\varphi$. Obviously, $1_H\in \mathrm{Im}\varphi$. Also, it can be seen from the proof of statement 2 that $h^{-1}=\varphi (g_1{)}^{-1}=\varphi (g_1^{-1})\in \mathrm{Im}\varphi$. Thus, $\mathrm{Im}\varphi <H$.

Note: Actually, $\ker \varphi ◃G$, as seen in the next lecture.

Theorem 4(Proposition).

Let $\psi :G\to G^{\prime }$ be a homomorphism of groups, and let $a$ and $b$ be elements of $G$. Let $K$ be the kernel of $\psi$. Then, the following are equivalent:

• $\psi (a)=\psi (b)$
• $a^{-1}b$ is in $K$
• $b$ is in the coset $aK$
• The cosets $bK$ and $aK$ are equal.

The last point can be proved by showing that $aK$ and $bK$ are subsets of each other.

Theorem 5(Proposition).

Let $K$ be the kernel of a homomorphism $\varphi :G\to G$. The fibre of $\varphi$ that contains an element $a$ of $G$ is the coset $aK$ of $K$. These cosets partition $G$, and they correspond to elements of the image of $\varphi$.