ALG2_L4

Isomorphisms

Definition 1(Definition).

Let $G=(G,\star )$ and $H=(H,\ast )$ be groups. A bijection $\varphi :G\to H$ is called an isomorphism if

$$\varphi (g_1\star g_2)=\varphi (g_1)\ast \varphi (g_2)\forall g_1,g_2\in G.$$

If there exists an isomorphism from $G$ to $H$, we say $G$ and $H$ are isomorphic and write $G\cong H$.

Theorem 2(Lemma).

If $\varphi :G\to G^{\prime }$ is an isomorphism, so is ${\varphi }^{-1}:G^{\prime }\to G$.

Note that ${\varphi }^{-1}$ is well defined because $\varphi$ is a bijection.

This lemma shows that when $\varphi$ is an isomorphism, we can make a computation in either group, then use $\varphi$ or ${\varphi }^{-1}$ to carry it over to the other. So, for computation with the group law, the two groups have identical properties. For example, if $g\in G$ has order $k$, then $\varphi (g)\in H$ also has order $k$. Similarly, if $G^{\prime }$ is a subgroup of $G$, then $\varphi (G^{\prime })$ is a subgroup of $H$ (this is also true for vanilla homomorphisms, but $\varphi$ being an isomorphism also guarantees $|G^{\prime }|=|\varphi (G^{\prime })|$).

Automorphisms

Recall that, if $\varphi :G_1\to G_2$ is a homomorphism,

• $\ker \varphi ◃G_1$, $\mathrm{Im}\varphi <G_2$.
• $\varphi$ is an isomorphism if $\ker \varphi =\{1_{G_1}\}$ and $\mathrm{Im}\varphi =G_2$.

$\varphi$ is called an automorphism if $G_1=G_2$. The set of all automorphisms is denoted by $\text{Aut }G\equiv \{\varphi :G\to G|\varphi \text{ is an isomorphism}\}$.

Theorem 3(Lemma).

Let $G$ be a group. Then, $\text{Aut }G$ is a group under composition.

Proof
The identity isomorphism is the identity element. Let ${\varphi }_1,{\varphi }_2\in \text{Aut }G$. Consider the map ${\varphi }_1{\varphi }_2$. Since ${\varphi }_1$ and ${\varphi }_2$ are bijective, ${\varphi }_1{\varphi }_2$ is too. It remains to show that ${\varphi }_1{\varphi }_2$ is a homeomorphism: $({\varphi }_1\circ {\varphi }_2)(g_1{g}_2)={\varphi }_1({\varphi }_2(g_1){\varphi }_2(g_2))={\varphi }_1({\varphi }_2(g_1)){\varphi }_1({\varphi }_2(g_2))=({\varphi }_1\circ {\varphi }_2)(g_1)({\varphi }_1\circ {\varphi }_2)(g_2)$. Thus, $\text{Aut }G$ is closed under composition. For any $\varphi \in \text{Aut }G$, ${\varphi }^{-1}$ is well defined and bijective, is a homomorphism (easy to check), and hence is an isomorphism: ${\varphi }^{-1}\in \text{Aut }G$.

Conjugation

The most important type of automorphism is conjugation: let $g$ be a fixed element of a group $G$. Conjugation by $g$ is the map $\varphi :G\to G$ defined by $x\mapsto gx{g}^{-1}$. This is an automorphism because, first of all, it is a homomorphism, and second, it is bijective because it have an inverse function: conjugation by $g^{-1}$.

Two elements $x,x^{\prime }\in G$ are called conjugates if $x=g{x}^{\prime }{g}^{-1}$ for some $g\in G$. Conjugates have similar algebraic behavior, since they are the images of each other under an isomorphism.

Theorem 4(Lemma).

If $H<G$, $g\in G$, then $gH{g}^{-1}<G$, and $gH{g}^{-1}\cong H$.

Proof
$gH{g}^{-1}$ is the image of a group under an homomorphism.

Theorem 5(Corollary).

If a group $G$ has just one subgroup $H$ of order $r$, then that subgroup is normal.

---

Projection maps

Theorem 6(Lemma).

Let $G$ be a group and $N◃G$. Then the map $\varphi :G\to G/N$ given by $g\mapsto gN$ is a surjective homomorphism.

$\varphi$ is known as the projection map.

Proof
$\varphi$ is clearly well-defined (each $g\in G$ maps to only coset in $G/N$). $\varphi$ is a homomorphism: $\varphi (g_1{g}_2)=g_1{g}_{2}N=(g_{1}N)(g_{2}N)=\varphi (g_1)\varphi (g_2)$. It is clearly surjective.

Note that $\ker \varphi =N$.

Exact chains

Note that in the above lemma, we have the following chain of homomorphisms, where $i_1,i_2$ and $i_3$ represent inclusion maps:

$$1_G\stackrel{i_1}{\to }N\stackrel{i_2}{\to }G\stackrel{\varphi }{\to }G/N\stackrel{i_3}{\to }{1}_{G/N}$$

Note that the image of one map is the kernel of the following map in the chain.

---

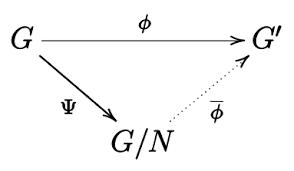
First isomorphism theorem

Theorem 7(Theorem).

Let $\varphi :G\to G^{\prime }$ be a homomorphism, and let $\psi :G\to G/\ker \varphi$ be a projection map. Then, there exists a unique injective homomorphism $\overline{\varphi }:G/\ker \varphi \to G^{\prime }$ such that $\varphi =\psi \circ \overline{\varphi }$. In other words, $G/\ker \varphi \cong \mathrm{Im}G$.

Proof
Define $\overline{\varphi }(g\ker \varphi )=\varphi (g)$. Note that $\overline{\varphi }$ is a unique, well defined, injective homomorphism.

---

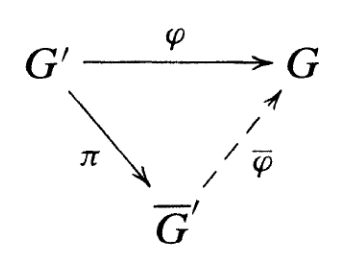
Mapping property of quotient groups

Theorem 8(Theorem).

Let $\phi :G^{\prime }\to G$ be a homomorphism, and let $N⊴G^{\prime }$ such that $N\subseteq \ker \phi$. Let ${\overline{G}}^{\prime }=G^{\prime }/N$, and let $\pi :G^{\prime }\to {\overline{G}}^{\prime }$ be the canonical projection map $a\mapsto \overline{a}$. The rule $\overline{\phi }(\overline{a})=\phi (a)$ defines a homomorphism $\overline{\phi }:{\overline{G}}^{\prime }\to G$, and $\overline{\phi }\circ \pi =\phi$.

This mapping property generalizes the first isomorphism theorem. The hypothesis that $N$ be contained in $\ker \phi$ is essential, of course.