ALG2_L6

Third isomorphism theorem

Theorem 1(Third Isomorphism Theorem).

Let $G$ be a group and let $H◃G$, $K◃G$, and $H<K$. Then, $K/H◃G/H$ and

$$\frac{G/H}{K/H}\cong G/K.$$

Proof
First, observe that $H◃G$ and $H<K<G$ implies $H◃K$. So, $K/H$ is a group.
Consider $kH\in K/H$, $gH\in G/H$.

$$\begin{array}{rl}(gH)(kH)(gH{)}^{-1}& =gHkH{g}^{-1}H\\ & =gk{g}^{-1}H\end{array}$$

Since $K$ is a normal subgroup, $gk{g}^{-1}\in K$. Thus, $gk{g}^{-1}H\in K/H$. Since conjugation is an invertible operation, this gives $(gH)(K/H)(gH{)}^{-1}=K/H$, i.e. $K/H◃G/H$.

Now, consider the map $\varphi :G/H\to G/K$ defined by $gH\mapsto gK$. This map is well defined, since if $g$ is in a coset $aK$, $gH$ is also necessarily in $aK$. $\varphi$ is also surjective, since for every $aK\in G/K$, $aH\mapsto aK$.

$\varphi$ is an homomorphism: $\varphi ((gH)\circ (g^{\prime }H))=g{g}^{\prime }K$, $\varphi (gH)\varphi (g^{\prime }H)=g{g}^{\prime }K$. The kernel of $\varphi$ is the set of all cosets of $H$ contained in $K$, $K/H$.

From the first isomorphism theorem, $\frac{G/H}{K/H}\cong G/K$.

Note that if only $H<G$, $K<G$, and $H<K$ are true, we can still define $\varphi :G/H\to G/K$ as we did above, but as a set theoretic function. Note that $G/H$ and $G/K$ are only sets of cosets here, not groups. Our reasoning that $\varphi$ is well defined did not use the normality of $H$ or $K$, and thus is still valid.

---

Direct products

Definition 2(Definition).

Let $G$ and $G^{\prime }$ be two groups. The product set $G\times G^{\prime }$, the set of pairs of elements $(a,a^{\prime })$ with $a$ in $G$ and $a^{\prime }$ in $G^{\prime }$, can be made into a group, known as the product group, by component wise multiplication:

$$(a,a^{\prime })(b,b^{\prime })=(ab,a^{\prime }{b}^{\prime }).$$

The pair $(1_G,1_{G^{\prime }})$ is the identity, and the inverse of $(a,a^{\prime })$ is $(a^{-1},a^{\prime -1})$. The associative law in $G\times G^{\prime }$ follows from the fact that it holds in $G$ and $G^{\prime }$.

The group $G\times G^{\prime }$ is related to $G$ and $G^{\prime }$ by inclusion and projection maps:

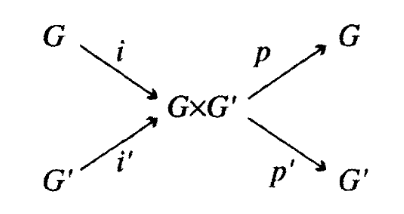
Here, $i$ is the inclusion map $g\mapsto (g,1_{G^{\prime }})$ and $p$ is the projection map $(g,g^{\prime })\mapsto g$. Ditto for $i^{\prime }$ and $p^{\prime }$.

Theorem 3(Proposition).

${\mathbb{Z}}_{mn}\cong {\mathbb{Z}}_m\times {\mathbb{Z}}_n$ when $(m,n)=1$.

Proof $(1,1)$ generates ${\mathbb{Z}}_m\times {\mathbb{Z}}_n$, and has order $mn$.

Recognizing direct products

Theorem 4(Theorem).

Let $H$ and $K$ be subgroups of a group $G$, and let $f:H\times K\to G$ be the multiplication map, defined by $f(h,k)=hk$. Its image is the set $HK=\{hk|h\in H,k\in K\}$.

1. $f$ is injective iff $H\cap K=\{1\}$.
2. $f$ is a homomorphism iff elements of $K$ commute with elements of $H$.
3. $HK<G$ iff $HK=KH$. Useful to note here that

• $H\le N_G(K)$ $⟹$ $HK=KH$.
• In particular, if $K◃G$, $HK=KH$ for all $H<G$.

4. $f$ is an isomorphism iff $H\cap K=\{1\}$, $HK=G$, $H◃G$, and $K◃G$.

Warning

Note that $HK=KH$ does not imply that the elements of $H$ commute with the elements of $K$. Also, 3.1 is not a two way implication.

Proof of 1
Let $H\cap K=\{1\}$. Then, $f(h,k)=f(h^{\prime },k^{\prime })⟹$ $hk=h^{\prime }{k}^{\prime }⟹$ $h^{\prime -1}h=k^{\prime }{k}^{-1}$. Notice that since $h^{\prime -1}h\in H$ and $k^{\prime }{k}^{-1}\in K$, it must be that both are equal to $1$. Thus, $h^{\prime -1}h=1⟹h^{\prime }=h$ and $k^{\prime }{k}^{-1}=1⟹k^{\prime }=k$.
On the other hand, if $g\in H\cap K$, $g\ne 1$, we have $(g,1)\mapsto g$ and $(1,g)\mapsto g$, making $f$ not injective.

Proof of 2

$$\begin{array}{rl}& f((h,k)\circ (h^{\prime },k^{\prime }))=f(h,k)\circ f(h^{\prime },k^{\prime })\\ ⟺& h{h}^{\prime }k{k}^{\prime }=hk{h}^{\prime }{k}^{\prime }\\ ⟺& h^{\prime }k=k{h}^{\prime }\forall h,h^{\prime }\in H,k,k^{\prime }\in K\end{array}$$

Proof of 3
3.1 and 3.2 should be obvious. Given $HK=KH$, $HK$ is closed under multiplication, since $HKHK=HHKK=HK$. Also, $(hk{)}^{-1}=k^{-1}{h}^{-1}$ is in $KH=HK$. The reverse implication is also easy to prove.

Proof of 4
The first two conditions ensure $f$ is injective and surjective, making it bijective. According to $(2)$, $f$ is a homomorphism iff $hk=kh$ for all $h\in H$ and $k\in K$. Consider the commutator $(k^{-1}hk)h^{-1}=k^{-1}(hk{h}^{-1})$. Since $H$ is normal, the left side is in $H$, and since $K$ is normal, the right side is in $K$. Knowing that $H\cap K=\{1\}$, we get $k^{-1}hk{h}^{-1}=1$.

Theorem 5(Proposition).

$$|HK|=\frac{|H||K|}{|H\cap K|}.$$

Proof
Notice that $HK$ is a union of a subset of the left cosets of $K$:

$$HK=\bigcup _{h\in h}hK.$$

Since each coset of $K$ had $|K|$ elements, it suffices to find the number of distinct cosets of the form $hK$, $h\in H$. But, $h_{1}K=h_{2}K$ $⟺$ $h_2^{-1}{h}_1\in K$ $⟺$ $h_2^{-1}{h}_1\in H\cap K$ $⟺$ $h_1(H\cap K)=h_2(H\cap K)$. Thus, $h_1$ and $h_2$ belong to the same coset of $K$ if and only if they also belong to the same coset of $H\cap K$. Thus, the number of distinct cosets of the form $hK$ is equal to the index of $H\cap K$ in $H$. Thus,

$$|HK|=\left(\frac{|H|}{|H\cap K|}\right)|K|.$$

---

Example: Chinese remainder theorem

Theorem 6(Chinese remainder theorem).

If positive integers $m$ and $n$ are co-prime,

$$\frac{\mathbb{Z}}{mn\mathbb{Z}}\cong \frac{\mathbb{Z}}{m\mathbb{Z}}\times \frac{\mathbb{Z}}{n\mathbb{Z}}.$$

Proof
Consider the map

$$\varphi :\frac{\mathbb{Z}}{mn\mathbb{Z}}\to \frac{\mathbb{Z}}{m\mathbb{Z}}\times \frac{\mathbb{Z}}{n\mathbb{Z}}$$

defined by

$$a+mn\mathbb{Z}\mapsto (a+m\mathbb{Z},a+n\mathbb{Z}).$$

Showing that $\varphi$ is well defined and is a homomorphism

To check that $\varphi$ is well defined, let $a_1+mn\mathbb{Z}=a_2+mn\mathbb{Z}$. Then, $a_1-a_2\in mn\mathbb{Z}$, i.e. $a_1-a_2=mnz$ for some $z\in \mathbb{Z}$. This can be rewritten an $a_1-a_2=m(nz)$, so, $a_1-a_2\in m\mathbb{Z}$. Thus, $a_1+m\mathbb{Z}=a_2+m\mathbb{Z}$. Similarly, $a_1+n\mathbb{Z}=a_2+n\mathbb{Z}$.

$\varphi$ is an homomorphism:

$$\begin{array}{rl}& \varphi ((a_1+mn\mathbb{Z})+(a_2+mn\mathbb{Z}))\\ & =\varphi (a_1+a_2+mn\mathbb{Z})\\ & =(a_1+a_2+m\mathbb{Z},a_1+a_2+n\mathbb{Z}).\end{array}$$ $$\begin{array}{rl}& \varphi (a_1+mn\mathbb{Z})+\varphi (a_2+mn\mathbb{Z})\\ & =(a_1+m\mathbb{Z},a_1+n\mathbb{Z})(a_2+m\mathbb{Z},a_2+n\mathbb{Z})\\ & =(a_1+a_2+m\mathbb{Z},a_1+a_2+n\mathbb{Z}).\end{array}$$

Establishing that $\ker \varphi =\text{lcm}(m,n)\mathbb{Z}/mn\mathbb{Z}$

The kernel of $\varphi$ is given by

$$\begin{array}{rl}& \ker \varphi \\ & =\{a+mn\mathbb{Z}|a+m\mathbb{Z}=m\mathbb{Z},a+n\mathbb{Z}=n\mathbb{Z}\}\\ & =\{a+mn\mathbb{Z}|a\in m\mathbb{Z},a\in n\mathbb{Z}\}\\ & =\{a+mn\mathbb{Z}|a\in m\mathbb{Z}\cap n\mathbb{Z}\}\\ & =\{a+mn\mathbb{Z}|a\in \text{lcm}(m,n)\mathbb{Z}\}\\ & =\frac{\text{lcm}(m,n)\mathbb{Z}}{mn\mathbb{Z}}.\end{array}$$

For the forward implication, since the size of the domain and codomain are equal, we only have to show either surjectivity or injectivity to have bijectivity. We can show injectivity right here: if $\text{lcm}(m,n)=mn$, $\ker \varphi =\{1\}$.

Alternatively, we can first prove a more general result:

Establishing that $\mathbb{Z}/\text{lcm}(m,n)\mathbb{Z}\cong \mathrm{Im}\varphi$

From the first isomorphism theorem,

$$\begin{array}{rl}& \frac{\mathbb{Z}/mn\mathbb{Z}}{\ker \varphi }\cong \mathrm{Im}\varphi \\ ⟹& \frac{\mathbb{Z}/mn\mathbb{Z}}{\text{lcm}(m,n)\mathbb{Z}/mn\mathbb{Z}}\stackrel{\overline{\varphi }}{\cong }\mathrm{Im}\varphi ,\end{array}$$

the isomorphism being defined by $\overline{\varphi }\left(a+\frac{\text{lcm}(m,n)\mathbb{Z}}{mn\mathbb{Z}}\right)=\varphi (a)$. From the third isomorphism theorem,

$$\frac{\mathbb{Z}}{\text{lcm}(m,n)\mathbb{Z}}\stackrel{\tilde{\varphi }}{\cong }\frac{\mathbb{Z}/mn\mathbb{Z}}{\text{lcm}(m,n)\mathbb{Z}/mn\mathbb{Z}}\stackrel{\overline{\varphi }}{\cong }\mathrm{Im}\varphi ,$$

with $\tilde{\varphi }$ being defined by $\tilde{\varphi }(a+\text{lcm}(m,n)\mathbb{Z})=a+\frac{\text{lcm}(m,n)\mathbb{Z}}{mn\mathbb{Z}}$. Thus, ${\varphi }_1\equiv \overline{\varphi }\circ \tilde{\varphi }$, ${\varphi }_1(a+\text{lcm}(m,n))=(a+m\mathbb{Z},a+n\mathbb{Z})$ is an isomorphism.

We can now show surjectivity by noting that $\mathrm{Im}\varphi$ must be isomorphic to a subgroup of $\mathbb{Z}/m\mathbb{Z}\times \mathbb{Z}/n\mathbb{Z}$ (which has order $mn$) of order $\text{lcm}(m,n)$. If $\text{lcm}(m,n)=mn$, the only subgroup $\mathrm{Im}\varphi$ can be isomorphic to is the entire codomain, making $\varphi$ surjective, and hence an isomorphism.

---

… or you could proceed like Clare did. We have the exact sequence

$$1_{\frac{\mathbb{Z}}{\text{lcm(m, n)}\mathbb{Z}}}\to \frac{\mathbb{Z}}{\text{lcm}(m,n)\mathbb{Z}}\stackrel{{\varphi }_1}{\to }\frac{\mathbb{Z}}{m\mathbb{Z}}\times \frac{\mathbb{Z}}{n\mathbb{Z}}$$

where ${\varphi }_1$ is injective (note that its codomain has been extended). We know that $\text{lcm}(m,n)=mn$ when $m$ and $n$ are co-prime, so let’s try to make ${\varphi }_1$ an isomorphism. To achieve this, all we need to do is to make ${\varphi }_1$ surjective. If we can construct another homomorphism ${\varphi }_2$ in the sequence such that $\mathrm{Im}{\varphi }_1=\ker {\varphi }_2$ and such that $\ker {\varphi }_2=\mathbb{Z}/m\mathbb{Z}\times \mathbb{Z}/n\mathbb{Z}$, we will be done.

Define

$${\varphi }_2:\frac{\mathbb{Z}}{m\mathbb{Z}}\times \frac{\mathbb{Z}}{n\mathbb{Z}}\to \frac{\mathbb{Z}}{m\mathbb{Z}+n\mathbb{Z}}$$

by ${\varphi }_2(a+m\mathbb{Z},b+n\mathbb{Z})=a-b+m\mathbb{Z}+n\mathbb{Z}$. (The notation here is a little misleading, so remember that $m\mathbb{Z}+n\mathbb{Z}$ is actually a product of two groups. It is a group since the multiplication map $f:m\mathbb{Z}\times n\mathbb{Z}\to \mathbb{Z}$ is a homomorphism. Since we are working with an abelian group, all subgroups are normal subgroups, so the quotient is defined).

To check ${\varphi }_2$ is well defined, let $(a_1+m\mathbb{Z},b_1+n\mathbb{Z})=(a_2+m\mathbb{Z},b_2+n\mathbb{Z})$. Then, $a_1-a_2\in m\mathbb{Z}$ and $b_1-b_2\in n\mathbb{Z}$. It follows that

$$\begin{array}{rl}& a_1-a_2-(b_1-b_2)\in m\mathbb{Z}+n\mathbb{Z}\\ ⟹& (a_1-b_1)-(a_2-b_2)\in m\mathbb{Z}+n\mathbb{Z}\\ ⟹& a_1-b_1+m\mathbb{Z}+n\mathbb{Z}=a_2-b_2+m\mathbb{Z}+n\mathbb{Z}.\end{array}$$

${\varphi }_2$ is a homomorphism:

$$\begin{array}{rl}{\varphi }_2(a_1+a_2+m\mathbb{Z},b_1+b_2+n\mathbb{Z})& =a_1+a_2-b_1-b_2+m\mathbb{Z}+n\mathbb{Z}\\ & ={\varphi }_2(a_1+m\mathbb{Z},b_1+n\mathbb{Z})+{\varphi }_2(a_2+m\mathbb{Z},b_2+n\mathbb{Z})\end{array}$$

Clearly, ${\varphi }_2$ is surjective, since ${\varphi }_2(k+m\mathbb{Z},n\mathbb{Z})=k+m\mathbb{Z}+n\mathbb{Z}$ for all $k\in \mathbb{Z}$ (this will be useful soon).

Now we will show that $\mathrm{Im}{\varphi }_1=\ker {\varphi }_2$.

$$\begin{array}{rl}& \mathrm{Im}{\varphi }_1=\{(a+m\mathbb{Z},a+n\mathbb{Z})|a\in \mathbb{Z}\},\\ & \ker {\varphi }_2=\{(a+m\mathbb{Z},b+n\mathbb{Z})|a-b\in m\mathbb{Z}+n\mathbb{Z}\}.\end{array}$$

$\mathrm{Im}{\varphi }_1\subseteq \ker {\varphi }_2$ should be obvious. If $(a+m\mathbb{Z},b+n\mathbb{Z})\in \ker {\varphi }_2$, $a-b=m{z}_1+n{z}_2$, i.e. $a-m{z}_1=b+n{z}_2=:c$. $(a+m\mathbb{Z},b+n\mathbb{Z})=(a-m{z}_1+m\mathbb{Z},b+n{z}_2+n\mathbb{Z})=(c+m\mathbb{Z},c+n\mathbb{Z})$. Thus, $\ker {\varphi }_2\subseteq \mathrm{Im}{\varphi }_1$.

Finally, we’ve got everything. If ${\varphi }_1$ is an isomorphism, $\ker {\varphi }_2=\mathrm{Im}{\varphi }_1=\mathbb{Z}/m\mathbb{Z}\times \mathbb{Z}/n\mathbb{Z}$, so $\mathrm{Im}{\varphi }_2=\left\{1_{\frac{\mathbb{Z}}{m\mathbb{Z}+n\mathbb{Z}}}\right\}$. Since ${\varphi }_2$ is surjective, $\frac{\mathbb{Z}}{m\mathbb{Z}+n\mathbb{Z}}=\mathrm{Im}{\varphi }_2$. This implies $m$ and $n$ generate $\mathbb{Z}$, which implies $\text{gcd}(m,n)=1$ or $\text{lcm}(m,n)=mn$.

Conversely, if $\text{gcd}(m,n)=1$, then $\frac{\mathbb{Z}}{m\mathbb{Z}+n\mathbb{Z}}$ is the trivial group, and $\mathrm{Im}{\varphi }_1=\ker {\varphi }_2=\frac{\mathbb{Z}}{m\mathbb{Z}}\times \frac{\mathbb{Z}}{n\mathbb{Z}}$, making ${\varphi }_1$ an isomorphism.