ALG2_L13

The free group

Definition 1(Definition).

A set of group elements that satisfy no relations except those implied by the axioms is called free, and a group that has a free set of generators is called a free group.

To construct a free group, start with an arbitrary set, say $S=\{a,b,\dots \}$. Let $S^{\prime }$ be the set that contains the symbols $a$ and $a^{-1}$ for every $a\in S$, $i$.$e$, $S^{\prime }=\{a,a^{-1},b,b^{-1},\dots \}$. The elements of $S^{\prime }$ are called symbols, and define a word to be a finite string of symbols, in which repetition is allowed. Let $W$ be the set of all words, with the empty string $e$. Define the product operation on $W$ to be concatenation. Obviously, $W$ is not a group, since inverses do not exist (yet).

If a word looks like $\dots x{x}^{-1}\dots$ for some $x\in S^{\prime }$, we may agree to “cancel” the two symbols $x$ and $x^{-1}$. Call a word reduced if no such reduction can be made. Starting with any $w\in W$, we can make a finite sequence of reductions to arrive at a reduced word $\overline{w}$, which is called the reduced form of $w$. There may be more than one way to arrive at the reduced word. If we want the notion of a reduced word to be well defined, we must ensure that all paths lead to $\overline{w}$.

Theorem 2(Theorem).

There is only one reduced word for a given word $w$.

Proof by induction on $n$ (easy). ref.

Define an equivalence relation $\sim$ on $W$ by $w\sim w^{\prime }$ if $w$ and $w^{\prime }$ have the same reduced word. Next, observe that products of equivalent words are equivalent, that is, $w\sim w^{\prime }$ and $v\sim v^{\prime }$ imply $wv\sim w^{\prime }{v}^{\prime }$. Therefore, it follows that the equivalence classes of words can be multiplied.

Theorem 3(Theorem).

The set $W/\sim$ of equivalence classes is a group, with the law of composition induced from multiplication in $W$.

Proof
The facts that multiplication is associative and that the class of the empty word $e$ is an identity follows from the corresponding facts in $W$. Also, for any $[xy\dots z]\in W/\sim$, $[z^{-1}\dots y^{-1}{x}^{-1}]\in W/\sim$ is clearly its inverse.

The group $W/\sim$ of equivalence classes in $S^{\prime }$ is called the free group on the set $S$, and is denoted by $\mathcal{F}(S)$.

Thus, for any group $S$, there exists a unique free group generated by $S$. Also, if $|S|=|T|$, the free groups generated by $S$ and $T$ are isomorphic. Thus, the free group of rank $r$ is defined.

From now on, we will not distinguish between any two words belonging to the same class in $W/\sim$ (words which are equivalent modulo the group axioms). Thus, “word” will refer to a class in $W/\sim$.

Generators and relations

Definition 4(Definition).

A relation among elements $x_1,x_2,\dots ,x_n$ of a group $G$ is a word $r$ in the free group on the set $\{x_1,x_2,\dots ,x_n\}$ that evaluates to $1$ in $G$.

Theorem 5(Theorem).

Let $R$ be a subset of a group $G$. There exists a unique smallest normal subgroup $N$ of $G$ which contains $R$, called the normal subgroup generated by $R$. If a normal subgroup of $G$ contains $R$, it contains $N$. The elements of $N$ can be described as follows: Let $R^{\prime }$ be the set consisting of elements $r$ and $r^{-1}$ with $r\in R$. An element of $G$ is in $N$ if it can be written as a product $y_1\dots y_r$ of some arbitrary length, where each $y_v$ is a conjugate of an element in $R^{\prime }$.

Definition 6(Definition).

Let $\mathcal{F}$ be the free group on a set $S=\{x_1,\dots ,x_n\}$, and let $R=\{r_1,\dots ,r_k\}$ be a set of elements of $\mathcal{F}$. The group generated by $S$ with relations $r_1,r_2,\dots ,r_k$ is the quotient group $\mathcal{G}=\mathcal{F}/\mathcal{R}$, where $\mathcal{R}$ is the normal subgroup of $\mathcal{F}$ generated by $R$. $\mathcal{G}$ is denoted by $⟨x_1,\dots ,x_n|r_1,\dots ,r_k⟩$.

Note that $\mathcal{R}$ is precisely the set of words in $\mathcal{F}$ which equate to the identity in $\mathcal{G}$. Let $R^{\prime }$ be the set consisting of elements $r$ and $r^{-1}$ with $r\in R$. Let $R^{\ast }$ be the set of all conjugates of the members of $R^{\prime }$: $\{xr{x}^{-1}|x\in \mathcal{F},r\in R^{\prime }\}$. Now, any word in $\mathcal{G}$ which evaluates to the identity can be expressed as a product of the elements of $R^{\ast }$. For example, if $p,q\in \mathcal{F}$, we know that the word $pq{r}_1{r}_3^{-1}{q}^{-1}{r}_2^4{p}^{-1}$ evaluates to the identity. It can be represented as a product of the members of $R^{\ast }$ as

$$(pq{r}_1{q}^{-1}{p}^{-1})(pq{r}_3^{-1}{q}^{-1}{p}^{-1})(p{r}_2^4{p}^{-1}).$$

Now, for $x\in \mathcal{F}$, consider the coset $x\mathcal{R}$. These are a set of words whose equivalence can be established using the relations $R$ (observe that since $\mathcal{R}$ is normal, $x\mathcal{R}$ contains every possible word equivalent to $x$ that you can think of: $x\mathcal{R}=\mathcal{R}x=\mathcal{R}x\mathcal{R}=\mathcal{R}{x}^2\mathcal{R}{x}^{-1}\mathcal{R}=\dots$). Thus, the cosets of $\mathcal{R}$ in $\mathcal{F}$ correspond to the distinct words in the group $\mathcal{G}$, modulo the relations in $R$.

Theorem 7(Mapping property of the Free group / universal property).

Let $\mathcal{F}$ be the free group on a set $S=\{a,b,\dots \}$, and let $G$ be a group. Any map of sets $f:S\to G$ extends uniquely to a group homomorphism $\phi :\mathcal{F}\to G$. If we denote the image $f(x)$ of an element $x$ of $S$ by $\overline{x}$ (and define $f(x^{-1})={\overline{x}}^{-1}$), the image of a word $w_1{w}_2\dots w_r\in \mathcal{F}$ will be $f(w_1)f(w_2)\dots f(w_r)$.

Theorem 8(Corollary).

Let $G$ be a group and $S=\{x_1,\dots ,x_n\}\subseteq G$. $R=\{r_1,\dots ,r_k\}$ is a set of relations among the elements of $S$ satisfied in $G$, $\mathcal{F}$ is a free group on $S$, and $\mathcal{R}$ is the normal subgroup of $\mathcal{F}$ generated by $R$. Let $\mathcal{G}=\mathcal{F}/\mathcal{R}$.
There is a canonical homomorphism $\psi :\mathcal{G}\to G$.

Proof
The mapping property gives us a homomorphism $\phi :\mathcal{F}\to G$ with $\phi (x_i)=x_i$. Clearly, $R\subseteq \ker \phi$. Since $\ker \phi$ is a normal subgroup and thus is closed under the operations we used to construct $\mathcal{R}$, $\mathcal{R}$ must also be contained in $\ker \phi$. The mapping property of quotient groups gives us a map $\overline{\phi }:\mathcal{G}\to G$. This is the map $\psi$.

Now,

1. $\psi$ is surjective iff $S$ generates $G$, and
2. $\psi$ is injective iff every relation among the elements of $S$ is in $\mathcal{R}$. In other words, $\psi$ is injective iff $\mathcal{R}=\ker \phi$.

$(1)$ is obvious; to see $(2)$, assume there exists a relation $\rho =1$ among the elements of $S$ which is not present in $\mathcal{R}$. Then, $\mathcal{R}$ and $\rho \mathcal{R}$ will be distinct cosets in $\mathcal{F}/\mathcal{R}$. However, both $\mathcal{R}$ and $\rho \mathcal{R}$ will be contained in $\ker \phi$. Thus, $\psi (\mathcal{R})=\psi (\rho \mathcal{R})=1$. Therefore, $\psi$ is not injective.

If the map $\psi$ is bijective, we say $R$ forms a complete set of relations among the generators $S$, and $G\cong \mathcal{G}$.

A more rigorous treatment

Alternatively, you can take the universal property to be the defining property of a free group, and then prove that our previous construction is indeed a free group by showing that it satisfies the universal property:

Definition 9(Definition).

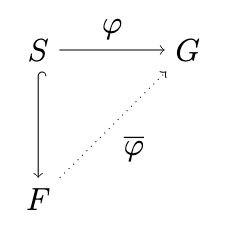
Let $S$ be a set. A free group $F$ generated by $S$ satisfies the following universal property: for any group $G$ and any function $\phi :S\to G$ there is a unique group homomorphism $\overline{\phi }:F\to G$ extending $\phi$, so that the following diagram commutes:

where the map from $S$ to $F$ is the inclusion map. We call $S$ a free generating set for $F$.

Here’s a roadmap:

• First, we will verify that the group we have constructed in the first section is indeed a free group.

• Then, we will prove that any two free groups generated by the same set S are isomorphic.

• This universality allows us to treat our specific construction as the free group on S, without loss of generality.

• Then, we will show that any two free generating sets of a free group $\mathcal{F}$ have the same cardinality, which is equal to $\text{rank}(\mathcal{F})$ (The rank of a group is the smallest cardinality of a generating set of the group).

• This allows us to define the “free group of rank $r$” to be a free group freely generated by a set of cardinality $r$.

• Finally, we will show that a group is finitely generated iff it is the quotient of a finitely generated free group.

Theorem 10(Theorem).

Let $S$ be a set. Consider the group $\mathcal{F}$ of equivalence classes of words on $S^{\prime }$ modulo the group axioms we constructed in the previous section. $\mathcal{F}$ is a free group.

Proof

To prove that $\mathcal{F}$ is a free group, we must verify that it satisfies the universal property. Let $G$ be an arbitrary group and $\phi :S\to G$ be any function. We need to construct a group homomorphism $\overline{\phi }:\mathcal{F}\to G$ and show it is unique and extends $\phi$. Since $\mathcal{F}$ is generated by the set $\{[\overline{a}]\mid a\in S\}$ (where $[\overline{a}]$ denotes the equivalence class of the word $a$), and every element of $\mathcal{F}$ is an equivalence class of reduced words formed by concatenating elements of $S^{\prime }=\{a,a^{-1}\mid a\in S\}$, we define $\overline{\phi }$ as follows:

• For $a\in S$, set $\overline{\phi }([\overline{a}])=\phi (a)$.
• For $a^{-1}\in S^{\prime }$, set $\overline{\phi }([\overline{a^{-1}}])=(\phi (a){)}^{-1}$, the inverse of $\phi (a)$ in $G$.
• For a general reduced word $[w]=[x_1{x}_2\cdots x_n]$ in $\mathcal{F}$, where each $x_i\in S^{\prime }$, define $\overline{\phi }([w])=\overline{\phi }([x_1])\cdot \overline{\phi }([x_2])\cdots \overline{\phi }([x_n])$, where the product is taken in $G$.

Note that $\overline{\phi }$ extends $\phi$ by construction. First, we must check that this is well-defined. Since elements of $\mathcal{F}$ are equivalence classes, $[w]=[w^{\prime }]$ if $w$ and $w^{\prime }$ reduce to the same reduced word via cancellations. The group structure of $G$ ensures that if $x_i{x}_{i+1}=e$ in $\mathcal{F}$ (e.g., $x_i=a$, $x_{i+1}=a^{-1}$), then $\overline{\phi }([x_i])\cdot \overline{\phi }([x_{i+1}])=\phi (a)\cdot (\phi (a){)}^{-1}=e_G$, the identity in $G$. Thus, the value of $\overline{\phi }([w])$ depends only on the equivalence class $[w]$, and the definition is consistent.

Next, we verify that $\overline{\phi }$ is a homomorphism. For $[w]=[x_1\cdots x_n]$ and $[v]=[y_1\cdots y_m]$ in $\mathcal{F}$, their product is $[w][v]=[x_1\cdots x_n{y}_1\cdots y_m]$, possibly after reduction. Then:

$$\begin{array}{rl}\overline{\phi }([w][v])& =\overline{\phi }([x_1\cdots x_n{y}_1\cdots y_m])\\ & =\overline{\phi }([x_1])\cdots \overline{\phi }([x_n])\cdot \overline{\phi }([y_1])\cdots \overline{\phi }([y_m])\\ & =\overline{\phi }([w])\cdot \overline{\phi }([v]),\end{array}$$

where any cancellations in the concatenation correspond to trivial products (e.g., $e_G$) in $G$. Thus, $\overline{\phi }$ is a group homomorphism.

Finally, we prove uniqueness. Suppose $\psi :\mathcal{F}\to G$ is another homomorphism satisfying $\psi \circ i=\phi$. Then, for each $a\in S$, $\psi ([\overline{a}])=\psi (i(a))=\phi (a)=\overline{\phi }([\overline{a}])$. Since $\{[\overline{a}]\mid a\in S\}$ generates $\mathcal{F}$, and $\psi$ and $\overline{\phi }$ are homomorphisms agreeing on the generators, they must agree on all of $\mathcal{F}$. Hence, $\mathcal{F}$ satisfies the universal property and is a free group generated by $S$.

Theorem 11(Theorem).

Let $S$ be a set. Then, up to isomorphism, there is only one free group generated by $S$.

Theorem 12(Theorem).

Let $\mathcal{F}$ be a free group and $S\subset F$ be a free generating set, then $\text{rank}(F)=|S|$.

Proof
By the universal property, for every function form $S$ to ${\mathbb{Z}}_2$, there is a homomorphism from $\mathcal{F}$ to ${\mathbb{Z}}_2$; conversely, every homomorphism can be defined this way (since $S$ generates $\mathcal{F}$ and the value of a homomorphism on $S$ determines it uniquely). Hence there are exactly $2^{|S|}$ homomorphisms from $\mathcal{F}$ to ${\mathbb{Z}}_2$. Now, let $S^{\prime }$ be another generating set of $\mathcal{F}$, not necessarily free. There are $2^{|S^{\prime }|}$ maps from $S^{\prime }$ to ${\mathbb{Z}}_2$. However, since $S^{\prime }$ is not a free generating set, not all of these will extend to well-defined homomorphisms. However, it still remains true that every homomorphism can be defined by a map from $S^{\prime }$ to ${\mathbb{Z}}_2$. Thus, there are at most $2^{|S^{\prime }|}$ homomorphisms from $\mathcal{F}$ to ${\mathbb{Z}}_2$. So, $2^{|S^{\prime }|}$ is an upper bound for $2^{|S|}$, and hence $|S^{\prime }|>|S|$. Thus, $|S|$ is the smallest cardinality of a generating set of $\mathcal{F}$, and $\text{rank}(\mathcal{F})=|S|$.

Theorem 13(Corollary).

All free generating sets of $F$ have the same cardinality. In other words, if $\mathcal{F}(X_1)\cong \mathcal{F}(X_2)$, then $|X_1|=|X_2|$.

Using this corollary and the uniqueness of free groups, we can finally define the free group of rank $r$.

Definition 14(Definition).

Let $r\in \mathbb{N}$ and let $S=\{x_1,\dots ,x_r\}$ where $x_1,\dots ,x_r$ are $r$ distinct elements. Then we write $F_r$ for the free group freely generated by $S$, and call it the free group of rank $r$.

Theorem 15(Theorem).

A group is finitely generated iff it is the quotient of a finitely generated free group.

Proof
By the first isomorphism theorem, this is equivalent to the statement: a group $G$ is finitely generated iff there exists a finitely generated free group $\mathcal{F}$ and a surjective homomorphism $\mathcal{F}\to G$. Note that a quotient of a finitely generated group is finitely generated (the image of the generators generate the image). Conversely, let $G$ be a finitely generated group, say generated by the finite set $S\subseteq G$. Let $\mathcal{F}$ be the free group generated by $S$, then $\mathcal{F}$ is finitely generated. From the universal property, we find a homomorphism $\phi :\mathcal{F}\to G$ that is identity on $S$ (hence surjective), then $G\cong F/\ker \phi$, as desired.