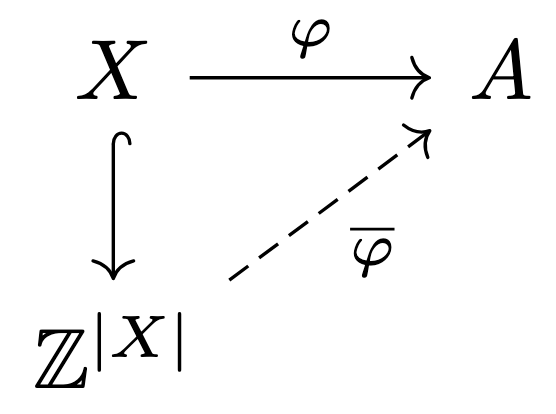ALG2_L14

Free abelian groups

The commutator subgroup of a group $G$, denoted by $[G,G]$, is defined to be $⟨ab{a}^{-1}{b}^{-1}|a,b\in G⟩$.

Theorem 1(Lemma).

For any group $G$, $[G,G]$ is a normal subgroup.

Proof
A subgroup is normal if $gh{g}^{-1}\in [G,G]$ for all $g\in G$, $h\in [G,G]$. Since $h$ is a product of commutators $c_i=a_i{b}_i{a}_i^{-1}{b}_i^{-1}$:

• Conjugate $c=ab{a}^{-1}{b}^{-1}$: $gc{g}^{-1}=$ $(ga{g}^{-1})(gb{g}^{-1})(g{a}^{-1}{g}^{-1})(g{b}^{-1}{g}^{-1})=$ $a^{\prime }{b}^{\prime }{a}^{\prime -1}{b}^{\prime -1}$, a commutator with $a^{\prime }=ga{g}^{-1}$, $b^{\prime }=gb{g}^{-1}$.
• For $h=c_1\cdots c_n$, $gh{g}^{-1}=(g{c}_1{g}^{-1})\cdots (g{c}_n{g}^{-1})$, a product of commutators, so $gh{g}^{-1}\in [G,G]$.
• Inverses follow similarly, as $(gc{g}^{-1}{)}^{-1}$ is a commutator.
  Hence, $[G,G]◃G$.

Theorem 2(Lemma).

If $\mathcal{F}$ is a free group, then $\mathcal{F}/[\mathcal{F},\mathcal{F}]$ is abelian.

Proof
Let $a[\mathcal{F},\mathcal{F}]$ and $b[\mathcal{F},\mathcal{F}]$ be any two elements in $\mathcal{F}$. Since $a^{-1}{b}^{-1}ab\in [\mathcal{F},\mathcal{F}]$, we have $ab[\mathcal{F},\mathcal{F}]=ba[\mathcal{F},\mathcal{F}]$.

Note that since the quotient of a finitely generated group is finitely generated (the images of the generators generate the image), if $\mathcal{F}$ is a finitely generated free group, $\mathcal{F}/[\mathcal{F},\mathcal{F}]$ is also finitely generated.

We will return to $\mathcal{F}/[\mathcal{F},\mathcal{F}]$ in a bit.

Definition 3(Definition).

A basis for an abelian group $A$ is a subset $X\subset A$ with the following properties:

1. $⟨X⟩=A$, that is, every $a\in A$ may be written as $a={\sum }_{x\in X}{n}_{x}x$ where $n_x\ne 0$ for only finitely many $x\in X$.
2. $X$ is independent, that is, for any collection of integers $\{n_x{\}}_{x\in X}$ such that only finitely many are nonzero we have

$$\sum _{x\in X}{n}_{x}x=0⟹n_x=0\text{ for all }x\in X.$$

We will restrict our development to abelian groups with finite bases, so just work with $⟨X⟩=A$ and $X$ being independent without the additional clauses.

Theorem 4(Theorem).

Let $A$ be an abelian group with finite basis $X$. Then every element $a\in A$ can be written uniquely as $a={\sum }_{x\in X}{n}_{x}x$, $n_x\in \mathbb{Z}$. The map $\Theta :{\mathbb{Z}}^{|X|}\to A$ given by $\Theta (\mathbf{n})={\sum }_{x\in X}{n}_{x}x$ is an isomorphism, and $A\cong {\mathbb{Z}}^{|X|}$.

Proof
It is easy to check that $\Theta$ is a homomorphism.

$$\begin{array}{rlr}\Theta (\mathbf{n}+\mathbf{m})& =\sum _{x\in X}(n_x+m_x)x& \\ & =\sum _{x\in X}{n}_{x}x+\sum _{x\in X}{m}_{x}x& (A\text{ is abelian})\\ & =\Theta (\mathbf{n})+\Theta (\mathbf{m}).& \end{array}$$

$\Theta$ is onto by property 1 of a basis, and has trivial kernel by property 2. Thus, $\Theta$ is an isomorphism, and unique linear decompositions of elements of $A$ in terms of $X$ follow.

Definition 5(Definition).

The group ${\mathbb{Z}}^{|X|}$ is called the free abelian group on $X$. It has a canonical basis $\{{\hat{e}}_x|x\in X\}$ which is in bijective correspondence with $X$.

Theorem 6(Theorem).

If $m,n$ are nonnegative integers with ${\mathbb{Z}}^m\cong {\mathbb{Z}}^n$, then $n=m$.

It follows that if $A$ is a free abelian group and $X$ and $Y$ are two bases for $A$, then $|X|=|Y|$.

Definition 7(Definition).

The free abelian group of rank $r$ is defined to be the free abelian group on the set $\{x_1,\dots ,x_r\}$, which is isomorphic to ${\mathbb{Z}}^r$.

The next theorem links free abelian groups with free groups.

Theorem 8(Theorem).

If $\mathcal{F}$ is the free group of rank $r$, then $\mathcal{F}/[\mathcal{F},\mathcal{F}]$ is the free abelian group of rank $r$.

Universal property of free abelian groups

Theorem 9(Theorem).

Let ${\mathbb{Z}}^{|X|}$ be the free abelian group on $X$. Let $i:X\to {\mathbb{Z}}^{|X|}$ be the function defined by $i(x)={\hat{e}}_x$. If $A$ is an abelian group and $\phi :X\to A$ is any map, then there exists a unique homomorphism $\overline{\phi }:{\mathbb{Z}}^{|X|}\to A$ that makes the following diagram commute:

This yields the following important corollary:

Theorem 10(Corollary).

Every abelian group is a quotient of a free abelian group.

Of interest to us is the finite case: if $A$ is a finitely generated abelian group generated by $n$ generators, then $A\cong {\mathbb{Z}}^n/H$ for some $H\le {\mathbb{Z}}^n$ (remember, all subgroups of an abelian group are normal).

It follows that to classify all the finitely generated abelian groups, we need only classify the subgroups $H$ of ${\mathbb{Z}}^n$ and their corresponding quotient groups.

Theorem 11(Invariant factor theorem).

If $H$ is a subgroup of a free abelian group $G$ or rank $n$, then $H$ is free abelian of rank $r\le n$. Further, there are bases $\{e_1,\dots ,e_n\}$ of $G$ and $\{d_1{e}_2,\dots ,d_r{e}_r\}$ of $H$ respectively where $d_i$ divides $d_{i+1}$ for $i<r$. The integers $d_i$ are uniquely determined up to sign and are called the invariant factors of $H$.

Theorem 12(Corollary: Structure theorem for finitely generated abelian groups).

A finitely generated abelian group is isomorphic to ${\mathbb{Z}}^m\times {\mathbb{Z}}_{d_1}\times \cdots \times {\mathbb{Z}}_{d_r}$ for some $m\ge 0$ and $d_i$ dividing $d_{i+1}$. The integer $m$ as well as all the $d_i$s (up to sign) are uniquely determined.

I’m having trouble understanding the invariant factor theorem. Consider the standard basis $e_1=(1,0,\dots ,0),e_2,\dots ,e_r$ for the free abelian group ${\mathbb{Z}}^r$. Let $H$ be the subgroup of ${\mathbb{Z}}^r$ generated by $\{e_1,2e_2,\dots ,r{e}_r\}$. Is it correct that the invariant factor theorem says that there exists another basis $e_1^{\prime },\dots ,e_r^{\prime }$ of ${\mathbb{Z}}^r$ such that $d_1{e}_1^{\prime },\dots ,d_r{e}_r^{\prime }$ is a basis of $H$ and $d_i$ divides $d_{i+1}$? If so, can you find me the basis?

Consider the standard basis $e_1=(1,0,\dots ,0),e_2,\dots ,e_r$ for the free abelian group ${\mathbb{Z}}^r$. Let $H$ be the subgroup of ${\mathbb{Z}}^r$ generated by $\{d_1{e}_1,\dots ,d_r{e}_r\}$ such that $d_i$ divides $d_{i+1}$. The invariant factor theorem says that the $d_i$s are uniquely determined up to sign.

Show that there does not exist a basis of ${\mathbb{Z}}^r$ such that the smallest positive integer that occurs as a coefficient in the expression of the elements of $H$ in terms of this basis is less than $d_1$.