CRS Theory of Computation

CMI, Aug-Nov 2025, C Aiswarya
Sipser (2013), Kozen (1997), Hopcroft et al. (2007)

\begin{array}{c}\Huge \equiv=\equiv_{M_{\equiv_{M_{\equiv_{M_{\equiv_{M_{\equiv_{M_{\equiv_{M_{\equiv_{.\,_{.\,_{.}}}}}}}}}}}}}}}\\\tiny{\textsf{Exhibit A: The Nerode Staircase}}\end{array}

---

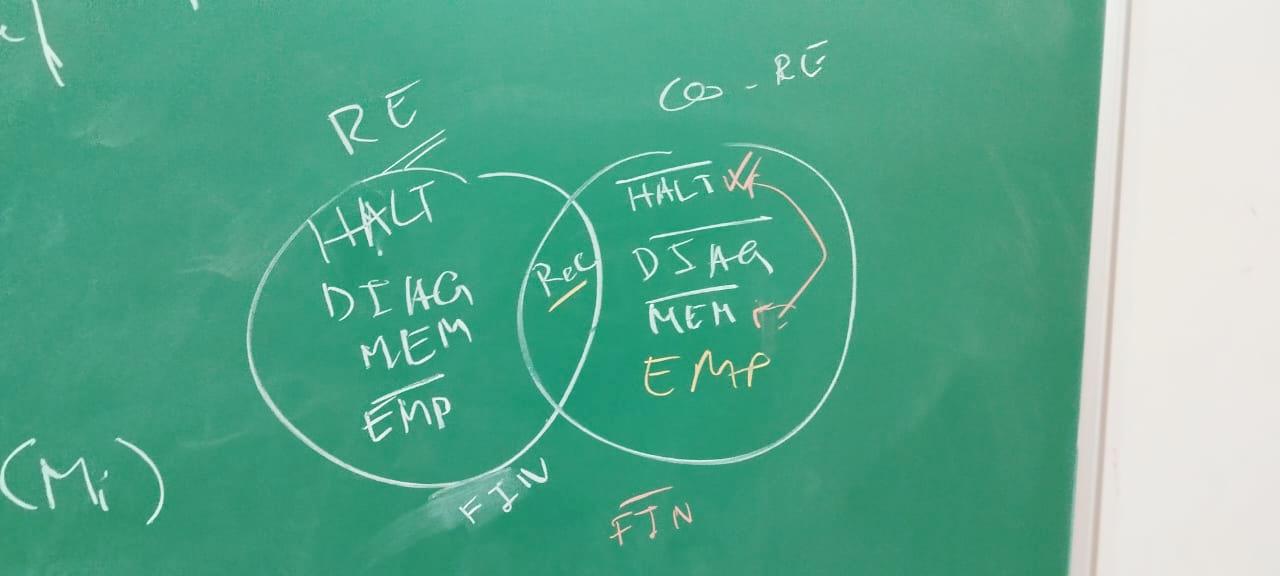
Automata and regular languages ✅ We show that automata and regular expressions describe the same class of languages.
When is a language regular ✅ Pumping Lemma, Ultimate periodicity of regular languages, Fooling sets.
The Myhill-Nerode Theorem Myhill-Nerode equivalence classes, the quotient relation, DFA minimization, uniqueness of minimal DFA
Algorithmic considerations for regular languages Complexity of translations between different formalizations, complexity of DFA minimization, algorithmic questions on finite representations of regular languages: membership, nonemptiness, universality, finiteness, intersection, nonemptiness, inclusion/containment, equivalence.
Context free grammars

Greybach normal form, CFGs as NPDAs, DPDAs weaker than NPDAs

LEC TOC 7

---

AS TOC 1
AS TOC 2
AS TOC 3
AS TOC 4

---

References

Hopcroft, J. E., Motwani, R., & Ullman, J. D. (2007). Introduction to Automata Theory, Languages, and Computation (3. ed). Pearson.

Kozen, D. C. (1997). Automata and Computability. Springer New York. https://doi.org/10.1007/978-1-4612-1844-9

Sipser, M. (2013). Introduction to the Theory of Computation (Third edition, international edition). Cengage Learning.