AS TOC 2

Problem 1

I will refer to the first and second languages by $L_1$ and $L_2$ respectively.

Claim 24.1(Claim).

$L_1=\{a,b{\}}^{\ast }$.

Proof.

e will induct on the length of words in$L_1$. $|ϵ{|}_a=|ϵ{|}_b$, so $ϵϵ=ϵ\in L_1$. Assume all words in $\{a,b{\}}^{\ast }$ of length $l$ are in $L_1$. Let $w\in \{a,b{\}}^{\ast }$ be of length $l+1$. We can write $w$ as $\overline{z}z$, where $\overline{z}\in \{a,b\}$, and $|z|=l$. By the induction hypothesis, we know $z\in L_1$, so there exist $x$ and $y$ such that $z=xy$ and $|x{|}_a=|y{|}_b$. If $\overline{z}=b$, we have $|bx{|}_a=|y{|}_b$ and $w=(\overline{z}x)y$, so $w\in L_1$. If $\overline{z}=a$, let $x=v\overline{v}$, where $\overline{v}\in \{a,b\}$. Note that $|\overline{z}v{|}_a=|\overline{v}y{|}_b$ holds for both values of $\overline{v}$. Since $w=(\overline{z}v)(\overline{v}y)$, $w\in L_1$.□

$L_1$ is regular, and hence recognizable.

Claim 24.2(Claim).

$L_2$ is not recognizable.

Proof.

\{ a^{n}\\ | \ n\geq 0 }$isafoolingset.Thedistinguishingsuffixbetween$a^{i}$$and$a^{j}$$is$b^{i}$:$a^{i}$b^{i}\in L_{2}$,but$a^{j}$b^{i}\notin L_{2}$.□

---

Problem 2

Consider the following $n$ state DFA, where a $\Sigma$-transition denotes a transition for every letter of the alphabet:

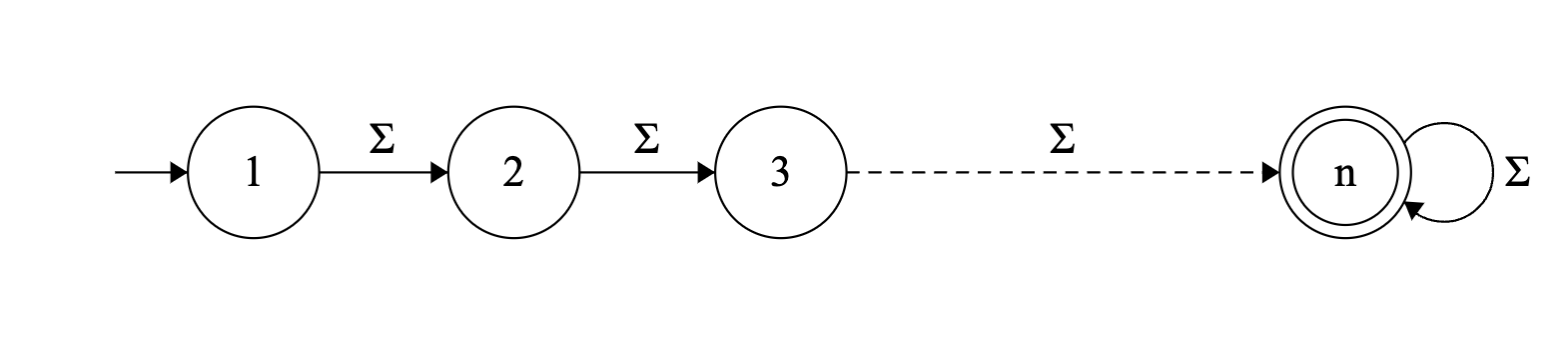
This accepts all words of length between $n$ and $2n$; in fact, it accepts all words of length $\ge n-1$. However, $L(A)\ne {\Sigma }^{\ast }$, since it does not accept any words of length less than $n-1$.

---

Problem 3

I will use the abbreviation a=ict. The production rule for $G$ becomes

$$\begin{array}{rl}& S\to aS|aSeS|s.\end{array}$$

$(a)$ Consider the word aases. This has two distinct parse trees in $P$:

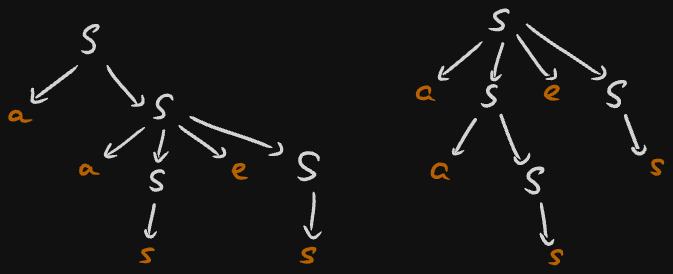
Thus, $G$ is ambiguous.

$(b)$ Let $G^{\prime }$ be the language $(\{R,M,U\},\{i,t,e,s,c\},P^{\prime },R)$, with the productions given by

$$\begin{array}{rl}& R\to U|M\\ & M\to s|aMeM\\ & U\to aR|aMeU.\end{array}$$

Every else must pair with the most recent unmatched if. The grammar enforces that only matched statements $M$ can appear between the if and else of an if-then-else clause. Any unmatched sub-statements $U$ are forced to appear after the else (for example, this makes the second parse tree above invalid in $P^{\prime }$). As a result, for any string in $L(G^{\prime })$, there is only one valid parse tree, eliminating ambiguity. Since every word in $L(G)$ can be derived using the productions in $G^{\prime }$ and vice versa, we have $L(G)=L(G^{\prime })$.