Automata and regular languages

Definition 26.1(Definition).

A finite automaton is a 5-tuple $(Q,\Sigma ,\delta ,q_0,F)$, where

1. $Q$ is a finite set of states,
2. $\Sigma$ is a finite set called the alphabet,
3. $\delta :Q\times \Sigma \to Q$ is the transition function,
4. $q_0\in Q$ is the start state, and
5. $F\subseteq Q$ is the set of accept states.

The set of all strings over an alphabet $\Sigma$ is denoted ${\Sigma }^{\ast }$. Any subset $L\subseteq {\Sigma }^{\ast }$ is called a language over the alphabet $\Sigma$. For nondeterministic finite automata, $\delta :Q\times {\Sigma }_{ϵ}\to 2^Q$.

If $A$ is the set of all strings that machine $M$ accepts, we say that $A$ is the language of machine $M$, denoted by $L(M)=A$.

We say that two automata are equivalent if they recognize the same language.

Theorem 26.2(Theorem).

Every nondeterministic finite automaton has an equivalent deterministic finite automaton.

Definition 26.3(Definition).

A language is called a recognizable language if some finite automaton recognizes it.

Most references calls these “regular languages”.

Definition 26.4(Definition).

Let $A$ and $B$ be languages. We define the regular operations union, concatenation, and star as follows:

1. $A\cup B\equiv \{x|x\in A\text{ or }x\in B\}$.
2. $A\circ B=\{xy|x\in A\text{ and }y\in B\}$.
3. $A^{\ast }=\{x_1\dots x_k|k\ge 0\text{ and each }{x}_i\in A\}$.

Note that $ϵ\in A^{\ast }$ for all $A$.

Theorem 26.5(Theorem).

The class of recognizable languages is closed under regular operations.

Proof.

Let$L_1$ and $L_2$ be regular languages recognized by $N_1$ and $N_2$ respectively.

Closure under union
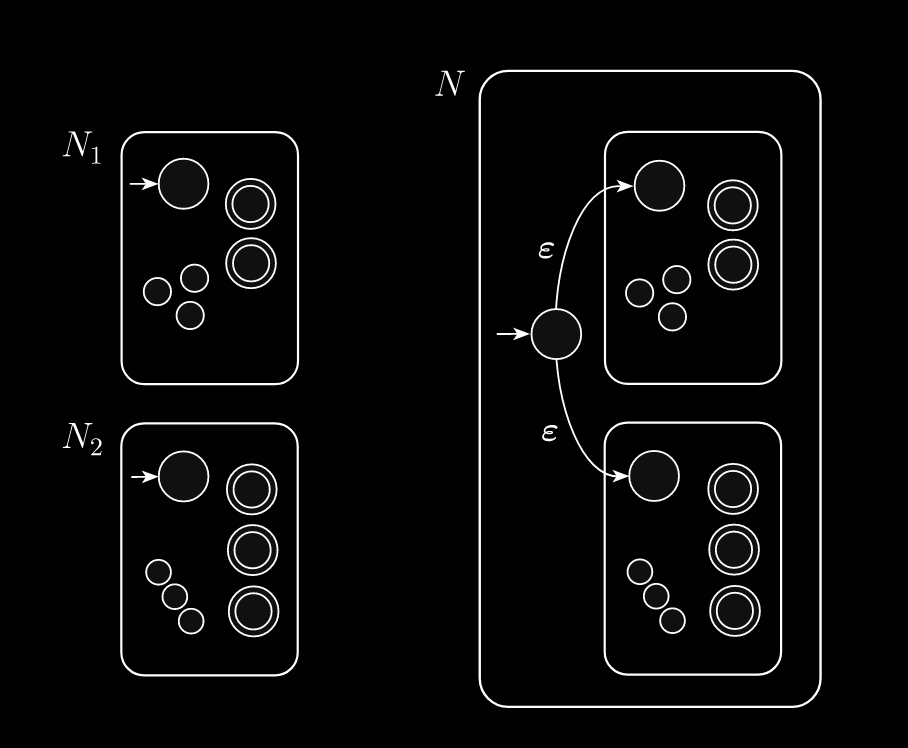
We have to demonstrate an $N$ which recognizes $L_1\cup L_2$. One method is to use the product construction and have $(q_1,q_2)\in Q_N$ be an accept state of $N$ if $q_1\in F_1$ or $q_2\in F_2$. Alternatively, use the following NFA construction:

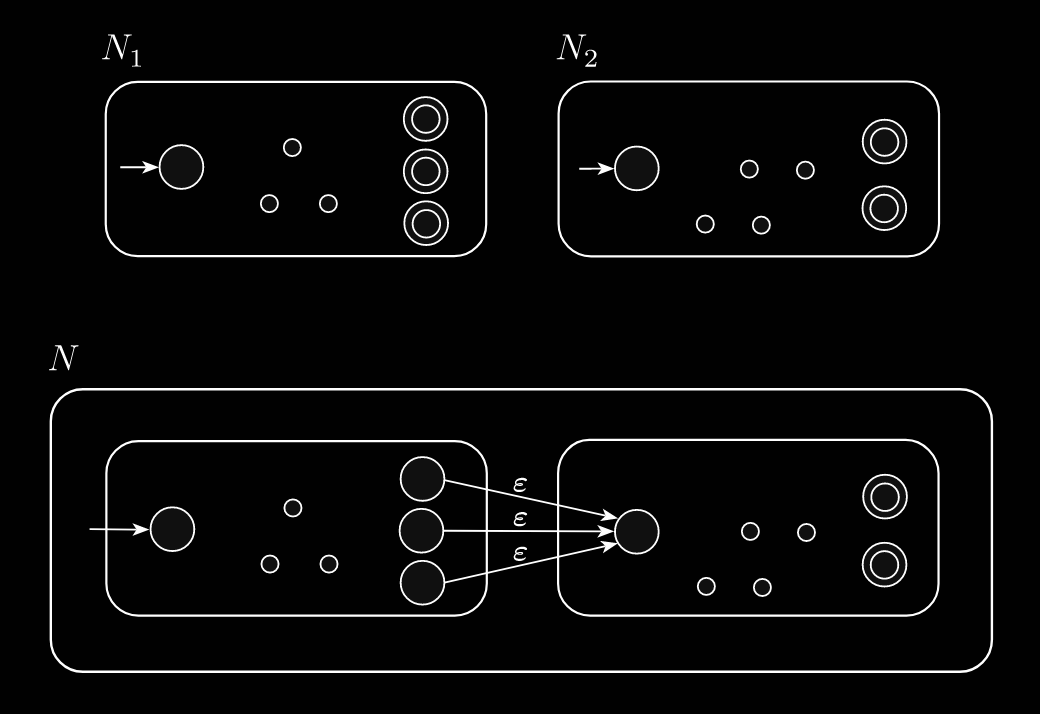
Closure under concatenation

Closure under star

□

172290

Definition 26.6(Definition).

Given an alphabet $\Sigma$, say that $R$ is a regular expression if $R$ is

1. $a$ for some $a\in \Sigma$,
2. $ϵ$,
3. $\varnothing$,
4. $(R_1\cup R_2)$, where $R_1$ and $R_2$ are regular expressions,
5. $(R_1{R}_2)$, where $R_1$ and $R_2$ are regular expressions, or
6. $(R_1^{\ast })$, where $R_1$ is a regular expression.

Definition 26.7(Definition).

Given an alphabet $\Sigma$, the set of rational languages are the smallest class of languages such that

1. it contains $\{ϵ\}$, $\varnothing$, and $\{a\}$ for all $a\in \Sigma$, and
2. it is closed under the regular operations.

3062b2

This is precisely the class of languages described by regular expressions.

Theorem 26.8(Theorem).

The class of recognizable languages is equal to the class of rational languages. That is, a language is recognized by a automaton iff it is described by a regular expression.

Proof.

Proving that a language described by a regular expression is recognizable is trivial: we can easily construct automata which recognize the languages in the first point of Definition 7, and we have already shown in Theorem 5 that recognizable languages are closed under regular operations.

See Sipser (2013) 1.60 for a proof of the converse using generalized nondeterministic finite automata (NFAs with REs labelling transition arrows instead of alphabets).□

Example 26.9(More NFA constructions).

A homomorphism is a function $h:{\Sigma }^{\ast }\to {\Gamma }^{\ast }$ such that $h(uv)=h(u)h(v)$, and $h(ϵ)=ϵ$.
Show that recognizable languages are also closed under intersection, complement, homomorphisms, and inverse homomorphisms.

Let $L_1$ and $L_2$ be regular languages recognized by $N_1$ and $N_2$ respectively.

Closure under complement

Complement $F_N$.

Closure under intersection

$L_1\cap L_2=(L_1\cup L_2{)}^c$. We have shown that recognizable languages are closed under union and complement. Alternatively, use the product construction, but make it such that $(q_1,q_2)\in Q_N$ is an accept state of $N$ if $q_1\in F_1$ and $q_2\in F_2$.

Closure under homomorphisms

First, we have to prove that if $L\subseteq {\Sigma }^{\ast }$ is a recognizable and $h:{\Sigma }^{\ast }\to {\Gamma }^{\ast }$ is a homomorphism, then $h(L)\subseteq {\Gamma }^{\ast }$ is also recognizable.

Let $A$ be an NFA over $\Sigma$ recognizing $L$. Replace every edge in $A$ labelled $a\in \Sigma$ with a path which reads $h(a)\in {\Gamma }^{\ast }$.

Next, we have to prove that if $M\subseteq {\Gamma }^{\ast }$ is recognizable, then $h^{-1}(M)\subseteq {\Sigma }^{\ast }$ is also recognizable.

Let $B$ be an NFA over $\Gamma$ recognizing $M$. Create a copy $B^{\prime }$ of $B$. Remove all transitions in $B^{\prime }$. Connect two states $\alpha ,\beta$ in $B^{\prime }$ with an arrow labelled $a\in \Sigma$ if $\beta$ can be reached from $\alpha$ on reading $h(a)$ in $B$.

6beea1

---

References

Sipser, M. (2013). Introduction to the Theory of Computation (Third edition, international edition). Cengage Learning.