AS TOC 3

Problem 1

Part a

Let $n$ be given by the pumping lemma for CFLs. Choose $w$ of length $>n$ such that $w=ab{a}^2{b}^2{a}^3{b}^3\dots$. Note that $w\#w\#\in L$. By the pumping lemma, we can write $w\#w\#=uvxyz$ such that $|vxy|\le n$ and $u{v}^{i}x{y}^{i}z\in L$ for all $i\ge 0$.

1. If $vxy$ is a substring of $w$, taking $i=0$ yields a word that is not in $L$.
2. If $\#\in x$, $\#\notin v,y$ since $|vxy|\le n$. If $y=ϵ$, take $i=0$. Otherwise, taking $i=0$ yields a word of the form $w^{\prime }\#w^{\prime \prime }\#$, where $w^{\prime }\ne w^{\prime \prime }$ is forced by our choice of $w$ and the fact that $vy\ne ϵ$.

Thus, $L$ is not context free.

Part b

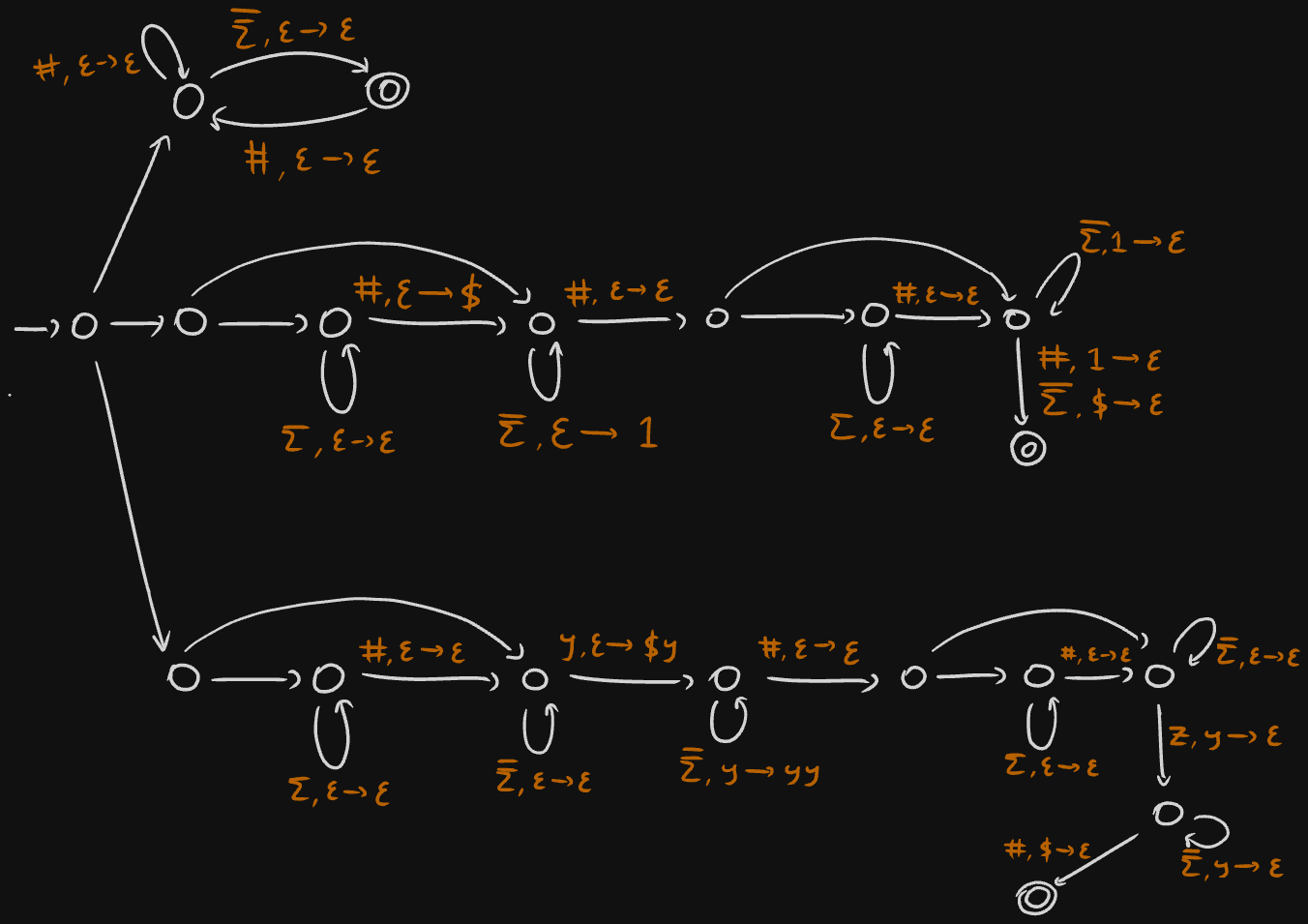
Unlabelled arrows are of type $ϵ,ϵ\to ϵ$. $\overline{\Sigma }$ represents $\{a,b\}$. The transition $z,y\to ϵ$ represents every transition of its type where $z\in \overline{\Sigma }$, $y\in \overline{\Sigma }$, and $z\ne y$.

---

Problem 2

Part a

Let $M=(Q,\Sigma ,\delta ,q_0,F)$ be a DFA recognizing $R$. For $q\in Q_0$, let $M_q=(Q\times \{0,1\},\Sigma ,{\delta }^{\prime },(q,0),(q,1))$, where

$$\begin{array}{rlr}{\delta }^{\prime }((p,0),a)& =(\delta (p,a),0)& a\in \Sigma \\ {\delta }^{\prime }((p,1),a)& =(\delta (p,a),1)& a\in \Sigma \\ {\delta }^{\prime }((f,0),ϵ)& =(q_0,1)& f\in F.\end{array}$$

Let

$$R^{\prime }=\bigcup _{q\in Q}L(M_q),$$

where $L(M_q)$ is the language of $M_q$. Since regular languages are closed under union, $R^{\prime }$ is regular. Suppose $w\in \text{cyclic}(R)$ such that $w=xy$ and $yx\in R$. If $\hat{\delta }(q_0,y)=q$, it follows that $w\in L(M_q)$, hence $w\in R^{\prime }$. Conversely, if $w\in L(M_q)$, $w$ can be expressed as $xy$ such that $\hat{\delta }(q,x)\in F$ and $\hat{\delta }(q_0,y)=q$, so $yx\in R$ and hence $xy\in \text{cyclic}(R)$. Thus, $\text{cyclic}(R)=R^{\prime }$ is regular (and hence also context free).

Part b

For context free $G$, $\text{cyclic}(G)$ is context free.

Let $\mathbf{G}=(\text{V},\Sigma ,\text{P},S)$ be a context free grammar for a language $G$ in CNF (I assume $ϵ\notin G$).

Let ${\text{V}}^{\prime }:=\{A^{\mathcal{R}},A^{\mathcal{L}}|A\in \text{V}\}\cup \{S_0\}$ be a collection of new non-terminals. For each pair of productions $A\to BC$ and $D\to AE$ in $\text{P}$, define productions

$$\begin{array}{rl}{A}^{\mathcal{R}}& \to D^{\mathcal{L}}B,\\ A^{\mathcal{L}}& \to C{D}^{\mathcal{L}}.\end{array}$$

For each pair of productions $A\to BC$ and $D\to EA$ in $\text{P}$, define productions

$$\begin{array}{rl}{A}^{\mathcal{R}}& \to D^{\mathcal{R}}B,\\ A^{\mathcal{L}}& \to C{D}^{\mathcal{R}}.\end{array}$$

For each production $S\to AB$ in $\text{P}$, define productions

$$\begin{array}{rl}{S}^{\mathcal{R}}& \to A,\\ S^{\mathcal{L}}& \to B.\end{array}$$

For each pair of productions $A\to BC$ and $C\to u$ in $\text{P}$ for some $u\in \Sigma$, define the production

$$\begin{array}{r}{S}_0\to u{A}^{\mathcal{R}}.\end{array}$$

For each pair of productions $A\to BC$ and $B\to u$ in $\text{P}$ for some $u\in \Sigma$, define the production

$$\begin{array}{r}{S}_0\to u{A}^{\mathcal{L}}.\end{array}$$

For each production $S\to u$ in $\text{P}$ for some $u\in \Sigma$, define the production $S_0\to u$.

Let ${\text{P}}^{\prime }$ be the set of newly defined productions. Let ${\mathbf{G}}^{\prime }=(\text{V}\cup {\text{V}}^{\prime },\Sigma ,{\text{P}}^{\prime },S_0)$.

Claim 25.1(Claim).

$L({\mathbf{G}}^{\prime })=\text{cyclic}(G)$.

Proof.

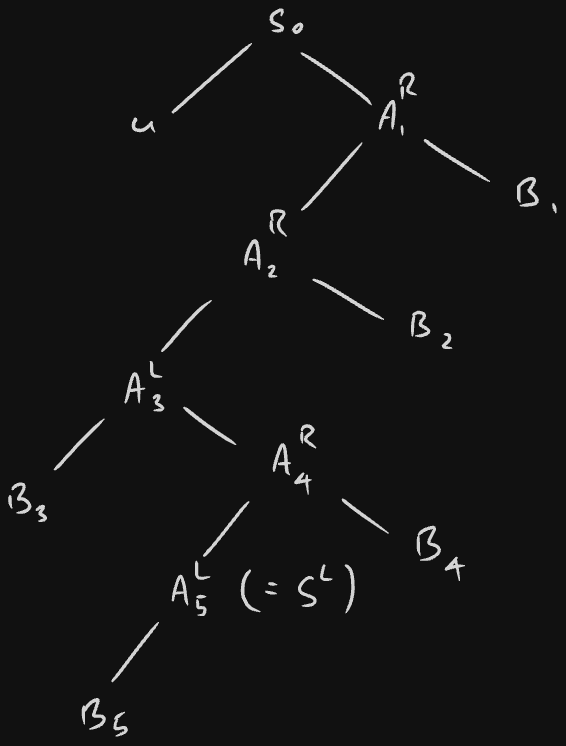
$(\subseteq )$ Suppose $w\in L({\mathbf{G}}^{\prime })$, and $u$ be the first letter of $w$. It is clear from the definition of ${\text{P}}^{\prime }$ that the derivation tree of $w$ must have a chain of non-terminals $S_0,{\tilde{A}}_1,{\tilde{A}}_2,\dots ,{\tilde{A}}_n$, where each ${\tilde{A}}_i\in {\text{V}}^{\prime }$, ${\tilde{A}}_i=A_i^{\mathcal{R}}$ or ${\tilde{A}}_i=A_i^{\mathcal{L}}$ for some $A_i\in \text{V}$, and $A_n=S$. Denote the child of ${\tilde{A}}_i$ not in ${\text{V}}^{\prime }$ by $B_i$. Here’s an example:

For $2\le i\le n$, depending on weather ${\tilde{A}}_i$ is $A_i^{\mathcal{R}}$ or $A_i^{\mathcal{L}}$, we have $A_i\to B_i{A}_{i-1}$ or $A_i\to A_{i-1}{B}_i$ in $\text{P}$ respectively. If ${\tilde{A}}_1=A_1^{\mathcal{R}}$, then $A_1\to B_{1}U\in \text{P}$, else if ${\tilde{A}}_1=A_1^{\mathcal{L}}$, then $A_1\to U{B}_1\in \text{P}$, where $U$ is such that $U\to u\in \text{P}$. Let ${\alpha }_1<{\alpha }_2<\cdots <{\alpha }_p$ be such that ${\tilde{A}}_{{\alpha }_i}=A_{{\alpha }_i}^{\mathcal{R}}$. Similarly, let ${\beta }_1<{\beta }_2<\cdots <{\beta }_q$ be such that ${\tilde{A}}_{{\beta }_i}=A_{{\beta }_i}^{\mathcal{L}}$. Then, we have the derivation

$$S=A_n\Rightarrow B_{{\alpha }_p}{B}_{{\alpha }_{p-1}}\dots B_{{\alpha }_1}u{B}_{{\beta }_1}{B}_{{\beta }_2}\dots B_{{\beta }_q}$$

in $\mathbf{G}$. It is clear from the derivation tree of $w$ that

$$S_0\Rightarrow u{B}_{{\beta }_1}{B}_{{\beta }_2}\dots B_{{\beta }_q}{B}_{{\alpha }_p}{B}_{{\alpha }_{p-1}}\dots B_{{\alpha }_1}$$

is a derivation in ${\mathbf{G}}^{\prime }$. Thus, we conclude that $w$ is a cyclic shift of a word in $L(\mathbf{G})$.

$(\supseteq )$ Suppose $w\in \text{cyclic}(G)$. Let $\overline{w}$ be the cyclic shift of $w$ such that $\overline{w}\in L(G)$. Suppose $w=xy$ and $\overline{w}=yx$. Let $u$ be the first letter of $x$, so $x=uz$.

Let $A_n,A_{n-1},\dots ,A_1,A_0$ be the chain of nonterminals in the derivation tree of $\overline{w}$ such that $A_n=S$ and $A_0=U\to u$ is a production in $\text{P}$. Let the child of $A_i$ which is not $A_{i-1}$ be $B_i$. Set ${\tilde{A}}_i=A_i^{\mathcal{R}}$ if $A_i\to B{A}_{i-1}$ and ${\tilde{A}}_i=A_i^{\mathcal{L}}$ if $A_i\to A_{i-1}B$ for $i\ge 1$. Let ${\alpha }_1<{\alpha }_2<\cdots <{\alpha }_p$ and ${\beta }_1<{\beta }_2<\cdots <{\beta }_q$ be as defined previously. Then, it again holds that

$$A_n\Rightarrow B_{{\alpha }_p}{B}_{{\alpha }_{p-1}}\dots B_{{\alpha }_1}u{B}_{{\beta }_1}{B}_{{\beta }_2}\dots B_{{\beta }_q}.$$

Further, it is evident that $B_{{\alpha }_p}{B}_{{\alpha }_{p-1}}\dots B_{{\alpha }_1}\Rightarrow y$ and $B_{{\beta }_1}{B}_{{\beta }_2}\dots B_{{\beta }_q}\Rightarrow z$. However, we also have the valid derivation

$$S_0\to u{\tilde{A}}_1\Rightarrow u{B}_{{\beta }_1}{B}_{{\beta }_2}\dots B_{{\beta }_q}{B}_{{\alpha }_p}{B}_{{\alpha }_{p-1}}\dots B_{{\alpha }_1}\Rightarrow uzy$$

in ${\mathbf{G}}^{\prime }$. Therefore, $w\in L({\mathbf{G}}^{\prime })$.□

Part c

Let $R=(abc{)}^{\ast }$.

$$R^{\prime }:=\text{permutation}(R)=\{w:|w{|}_a=|w{|}_b=|w{|}_c\}.$$

If $R^{\prime }$ were context free, then $R^{\prime }\cap (a^{\ast }{b}^{\ast }{c}^{\ast })=\{a^n{b}^n{c}^n:n\ge 0\}$ would be context free, a contradiction. Thus, $\text{permutation}(R)$ for regular $R$ is not context free in general.

Part d

Every regular language is context free. Thus, by the previous problem, $\text{permutation}(G)$ is not context free.