DMAT_PS1

Problem sheet 1.

1

The binary sequences in $\{0,1{\}}^{\mathbb{N}}$ can be represented as subsets of $\mathbb{N}$, with the nth bit deciding on whether $n$ is in the subset.

1 a

$\{\{1\},\{1,2\},\{1,2,3\},\dots \}$

1 b

$\{\{1\},\{2\},\{3\},\dots \}$

1 c

Find an uncountable antichain in $\{0,1{\}}^{\mathbb{N}}$

Let $a$ represent $01$, and $b$ represent $10$. Let $A$ be the set of all sequences of $a$s and $b$s. Note that a bijection between $A$ and $\{0,1{\}}^{\mathbb{N}}$ exists, so $A$ is uncountable. Also, no two elements in $A$ are comparable.

1 d

Solution using Dedekind cuts

We know that $\mathbb{Q}$ is countable. Let $\varphi :\mathbb{Q}\to \mathbb{N}$ be a bijection. We know that every real number is uniquely determined by a Dedekind cut in $\mathbb{Q}$. So, for $r\in \mathbb{R}$, define

$$\psi (r)=\{\varphi (q)|q<r\}.$$

$\mathbb{R}$ is uncountable, and $\psi$ associates each $r\in \mathbb{R}$ with a unique subset of $\mathbb{N}$ such that $\psi (r)\subset \psi (r^{\prime })$ whenever $r<r^{\prime }$.

Alternate solution due to Negi

Associate each $r\in (0.1,1)$ with a subset of $\mathbb{N}$ like exemplified:

$$\begin{array}{rl}\varphi (0.7184\dots )=& \{\\ & 1,2,3,4,5,6,7,\\ & 10,11,12,\dots ,71,\\ & 100,101,102,\dots ,718,\\ & ⋮\\ & \}\end{array}$$

1 e

Solution using a tree structure

Construct a binary tree and associate each point with a natural number like so:

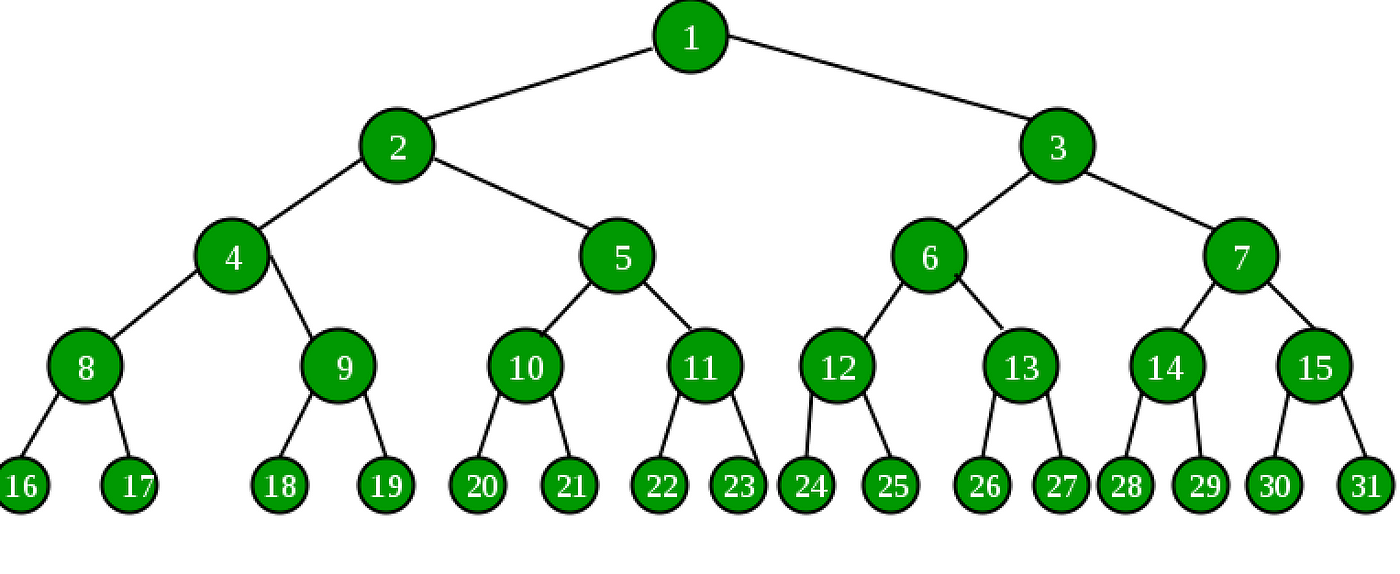
(The tree is infinite)

Now, with each node of the tree, associate a subset of $\mathbb{N}$ which consists of all the numbers of the nodes in the path between the node and the root of the tree. For example, the subset associated with 26 would be $\{1,3,6,13,26\}$. Consider the set of all sets associated with every node in the tree. The intersection of any two elements of this set must necessarily have a finite intersection, since the paths to the two nodes corresponding to the elements must diverge at some point.

Alternate solution due to Negi

Associate each $r\in (0.1,1)$ with a subset of $\mathbb{N}$ as exemplified:

$$\begin{array}{rl}\varphi (0.13514\dots )=& \{1,13,135,1351,\dots \}\end{array}$$

---

2

2 a

Consider all the functions which have $f(0)=k$. Then, the function can decrease its value by 1 at most $k$ times. Thus, we can associate the function with a k-tuple which records when the function performs the k-th drop. If the function settles at a constant value $v>0$, then we can fill the unused $v$ spots with zeroes. For example, the function

$$f(x)=\{\begin{array}{ll}5& 0\le x<6\\ 4& 6\le x<11\\ 2& 11\le x<100\\ 1& 100\le x\end{array}$$

would be associated with the tuple $(6,11,11,100,0)$. Note that ${\bigcup }_{n\in \mathbb{N}}{\mathbb{N}}^n$ is countable. We have an injection from the set of all non increasing functions from $\mathbb{N}$ to $\mathbb{N}$ to ${\bigcup }_{n\in \mathbb{N}}{\mathbb{N}}^n$. Thus, the set in question is countable.

2 b

A non decreasing function from $\mathbb{N}$ to $\mathbb{N}$ can be bijected to ${\mathbb{N}}^{\mathbb{N}}$. Associate each such function $f$ with the infinite tuple $(f(0),f(1)-f(0),f(2)-f(1),\dots )$. Thus, the set is uncountable.

2 c

Let $S$ be the set of all injective functions form $\mathbb{N}$ to $\mathbb{N}$. We can construct an injection from ${\mathbb{N}}^{\mathbb{N}}$ to $S$ like so: with $(a_1,a_2,a_3,\dots )\in {\mathbb{N}}^{\mathbb{N}}$, associate the function

$$\begin{array}{rl}& f(0)=a_1\\ & f(1)=f(0)+a_2+1\\ & f(2)=f(1)+a_2+1\\ & ⋮\end{array}$$

$f$ is clearly injective, and unique to $(a_1,a_2,a_3,\dots )$. Thus, $|S|\ge |{\mathbb{N}}^{\mathbb{N}}|$, i.e, $S$ is uncountable.

2 d

Let $S$ be the set of all surjective functions from $\mathbb{N}$ to $\mathbb{N}$. We can construct an injection from ${\mathbb{N}}^{\mathbb{N}}$ to $S$ like so: with $(a_1,a_2,a_3,\dots )\in {\mathbb{N}}^{\mathbb{N}}$ associate a function like so:

$$\begin{array}{r}f(x)=\{\begin{array}{ll}1& 1\le x<1+a_1\\ 2& 1+a_1\le x<1+a_1+a_2\\ ⋮& \end{array}\end{array}$$

Thus, $|S|\ge |{\mathbb{N}}^{\mathbb{N}}|$, i.e, $S$ is uncountable.

2 e

A Cantor diagonalization argument is a simple way to show that the set of all bijections from $\mathbb{N}$ to $\mathbb{N}$ is uncountable.

Alternate solution using the Riemann rearrangement theorem

The Riemann rearrangement theorem states that for any conditionally convergent series ${\sum }_{n=1}^{\infty }{a}_n$ (e.g., the alternating harmonic series ${\sum }_{n=1}^{\infty }\frac{(-1{)}^{n+1}}{n}$), the terms can be rearranged (via a permutation of $\mathbb{N}$) to converge to any real number, or even diverge to $\pm \infty$.

By the above theorem, for every real number $r$, there must exist at least one permutation ${\sigma }_r:\mathbb{N}\to \mathbb{N}$ such that

$$\sum _{n=1}^{\infty }{a}_{{\sigma }_r(n)}=r.$$

Thus, the set of all bijections from $\mathbb{N}$ to $\mathbb{N}$ is uncountable.

---

3

Consider the set of all binary sequences, $\{0,1{\}}^{\mathbb{N}}$. Replace $0$ with $00$ and $1$ with $01$.

---

4

The Hausdorff maximal principle: Let $S$ be a partially ordered set. Then $S$ contains a maximal chain (i.e. a chain which is not contained in a bigger chain).

Let $\mathbf{C}$ be the set of all chains in $S$. Define a partial order $\le$ on $\mathbf{C}$ such that $C_1\le C_2$ iff $C_1\subset C_2$. Let $\mathcal{C}$ be a chain in $(\mathbf{C},\le )$. Let $C^{\prime }\equiv {\bigcup }_{C\in \mathcal{C}}C$. Any two elements in $C^{\prime }$ are in some $C\in \mathcal{C}$, and are hence comparable, making $C^{\prime }$ a chain in $S$, i.e. $C^{\prime }\in \mathbf{C}$. It is evident that $C^{\prime }$ is an upper bound for $\mathcal{C}$. Thus, every chain in $S$ has an upper bound. From Zorn’s Lemma, $S$ has a maximal element, i.e, a chain $\overline{C}$ which is not contained in any other chain.

---

5

Let $\mathcal{F}$ be a filter on $X$. We have to show that it is contained in an ultrafilter. Let $K_{\mathcal{F}}$ be the set of all filters on $X$ which contain (are supersets of) $\mathcal{F}$. Define a partial order $\le$ on $K_{\mathcal{F}}$ by ${\mathcal{F}}_1\le {\mathcal{F}}_2$ iff ${\mathcal{F}}_1\subset {\mathcal{F}}_2$. Consider a chain $C$ in $K_{\mathcal{F}}$. Let $\hat{\mathcal{F}}={\bigcup }_{{\mathcal{F}}^{\prime }\in C}{\mathcal{F}}^{\prime }$. It is easily verified that $\hat{\mathcal{F}}$ is a filter on $X$ and $\hat{\mathcal{F}}$ contains $\mathcal{F}$, i.e. $\hat{\mathcal{F}}\in K_{\mathcal{F}}$. Thus, every chain in $(K_{\mathcal{F}},\le )$ has an upper bound. From Zorn’s lemma, $(K_{\mathcal{F}},\le )$ must have a maximal element $\overline{\mathcal{F}}$.

We will now show that $\overline{\mathcal{F}}$ is an ultrafilter. Suppose not. Let $C\in X$ such that $C\notin \overline{\mathcal{F}}$ and $X\setminus C\notin \overline{\mathcal{F}}$. Note that for all $A\in \overline{\mathcal{F}}$, $A\cap C\ne \varnothing$. Define $\tilde{\mathcal{F}}\equiv \{Y\subset X|\exists A\in F,A\cap C\subset Y\}$. Clearly, $\overline{\mathcal{F}}\subset \tilde{\mathcal{F}}$. It is easy to verify that $\tilde{\mathcal{F}}$ is a filter. Thus, $\tilde{\mathcal{F}}\in K_{\mathcal{F}}$ and $\overline{\mathcal{F}}\le \tilde{\mathcal{F}}$, which contradicts the maximality of $\mathcal{F}$.

---