LEC ALGO 3

Recursion trees

Refer Erickson (2019, p. 32)

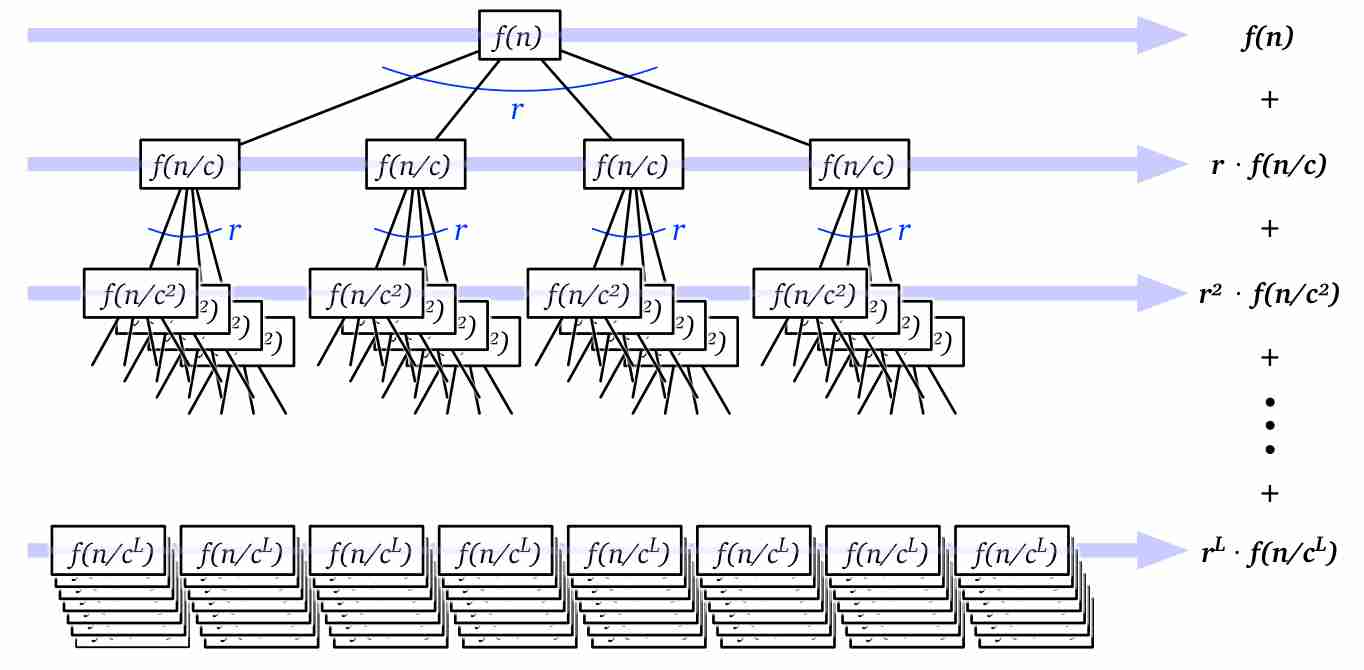
Consider the recurrence

$$T(n)=rT\left(\frac{n}{c}\right)+f(n),$$

where $r>0$, $c>1$, and $f(n)$ is asymptotically positive. $T(n)$ is the sum of all values in the recursion tree; evaluating this sum level by level, we obtain

$$T(n)=\sum _{i=0}^L{r}^i\cdot f(n/c^i)$$E1

where $L$ is the depth of the tree. If we take $n_0=1$ to be our base case, we have $L={\log }_{c}n$. This means that we have $r^L=n^{{\log }_{c}r}$ leaves in the recursion tree, and the last term in (E1) is $n^{{\log }_{c}r}f(1)=O(n^{{\log }_{c}r})$.

Three common cases:

1. If the series decays exponentially - every term is a constant factor smaller than the previous term - then it follows from the properties of geometric series that $T(n)=O(f(n))$. In this case, the sum is dominated by the value at the root of the tree.
2. If all terms in the series are equal, we have $T(n)=O(f(n)\cdot L)=O(f(n)\log n)$.
3. If the series grows exponentially - every term is a constant factor larger than the previous term - then $T(n)=O(n^{{\log }_{c}r})$. In this case, the sum is dominated by the number of leaves in the recursion tree.

Example 120.1(Example).

For case 1, take

$$T(n)=2T\left(\frac{n}{4}\right)+n.$$

Then, $T(n)={\sum }_{i=0}^{L}n/2^i<2n=O(n)$.

---

Another example:

$$T(n)=6T\left(\frac{n}{3}\right)+n^2\log n.$$ $$T(n)=\sum _{i=0}^L{\left(\frac{2}{3}\right)}^i{n}^2\log \left(\frac{n}{3^i}\right).$$

If $t_i$ is the $i$th term in the sequence, it is clear that $t_{i+1}<\frac{2}{3}{t}_i$. Thus, $T(n)=O(n^2\log n)$.

---

For case 2, consider the recurrence for merge sort:

$$T(n)=2T\left(\frac{n}{2}\right)+n.$$

$T(n)={\sum }_{i=0}^{L}n=O(nL)=O(n\log n)$.

---

As a more general example, take

$$T(n)=aT\left(\frac{n}{b}\right)+n^d,$$

for some $r>0$ and $c>1$.

$$T(n)=\sum _{i=0}^L{a}^i{\left(\frac{n}{b^i}\right)}^d=n^d\sum _{i=0}^L\frac{a^i}{b^{id}}.$$

If $a/b^d>1$, then $T(n)=O(a^L)=O(n^{{\log }_{b}a})$. If $a/b^d<1$, then $T(n)=O(n^d)$. If $a/b^d=1$, then $T(n)=O(n^d\log n)$.

Understanding cases 1, 2, and 3 by varying $r$ and $c$ for a fixed $f$ is easy, as seen in ^ddb755. How does varying $f$ affect $O(T(n))$? Roughly speaking, if $f$ grows faster, we gravitate toward case 1, and vice versa. For example, consider the merge sort recurrence again. For $f(n)=n$, we were in case 2. What happens if we have $f(n)=n^2$ instead?

$$T(n)=\sum _{i=0}^L{2}^i{\left(\frac{n}{2^i}\right)}^2=n^2\sum _{i=0}^L\frac{1}{2^i},$$

so we’re now in case 1, and $O(T(n))=O(f(n))=O(n^2)$. What about $f(n)=\sqrt{n}$?

$$T(n)=\sqrt{n}\sum _{i=0}^L{2}^{i/2},$$

we’re in case 3, and $O(T(n))=O(n^{{\log }_{2}2})=O(n)$.

We can make this more precise. Let $n^{{\log }_{c}r}$ be the critical exponent. Then,

1. If $f(n)=\Omega (n^{{\log }_{c}r+ϵ})$ for some $ϵ>0$, and if $af(n/b)\le cf(n)$ for some $c<1$ and all large $n$, then $T(n)=\Theta (f(n))$.
2. If $f(n)=\Theta (n^{{\log }_{c}r}{\log }^{k}n)$ for some $k\ge 0$, then $T(n)=\Theta (n^{{\log }_{c}r}{\log }^{k+1}n)$.
3. If $f(n)=O(n^{{\log }_{c}r-ϵ})$ for some $ϵ>0$, then $T(n)=\Theta (n^{{\log }_{c}r})$.

[!Reminder] Ask Vardhan for a proof of this

---

References

Erickson, J. (2019). Algorithms (1st paperback edition). Selbstverlag.