CMI, Aug-Nov 2025, Siddharth Pritam
Cormen et al. (2009), Erickson (2019)
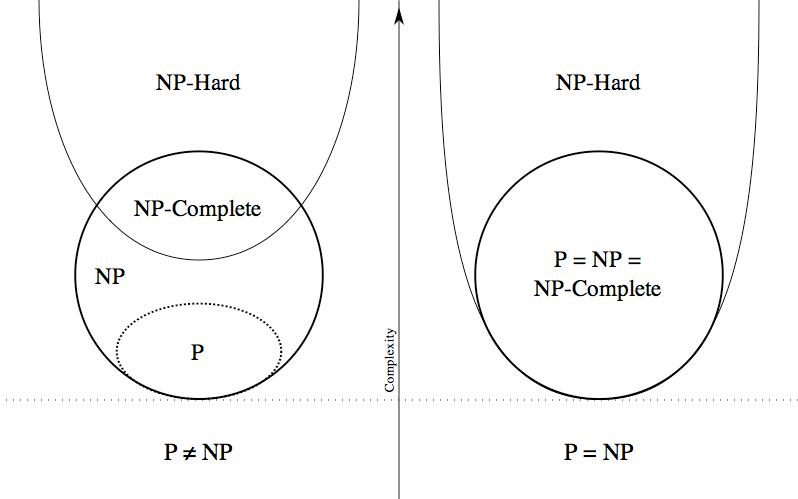
Lectures
LEC ALGO 3 ✅ Recursion trees, the master theorem
LEC ALGO 4 Divide and conquer: the convex hull problem
LEC ALGO 5 QuickSelect, find closest points in a collection
LEC ALGO 6 BSTs, quicksort, shellsort, radix sort, bucket sort
(using BST instead of an array makes insertion sort go from a O(n^2) to O(n log n) algorithm)
LEC ALGO 7 Heaps, heapsort, comparison based sorting algorithms cannot be faster than
Probabilistic Analysis and Randomized Algorithms
LEC ALGO 8 Hash tables, simple uniform hashing, open addressing, linear and quadratic probing
LEC ALGO 9 When being greedy works - Prim’s algorithm
LEC ALGO 10 Huffman codes
12/9: Hash table: a way to store key/value pairs and access/insert/delete them in O(1) time. The idea is to map keys to an array {0…m-1} with a hash function, but key collision issues arise. Linked lists are used to solve this problem. Also talked about how SUH (simple uniform hashing) functions are best (because there’s roughly an equal chance of a key mapping to any of the m slots.)
17/9: Hash table with Open Addressing instead of linked lists. One slot of the {m} array only ever has one key, if a collision is found, a new slot is found every time with a special kind of hash function facilitating this. the function that decides what slot to look for next when a slot is full, is a probing function. Linear and quadratic probing functions were discussed
19/9: Greedy algorithms, a technique for optimization: involves finding optimal solutions to a SUBproblem and using it to find an optimal solution to the problem. Example of a greedy algorithm for finding minimal spanning tree of a graph was covered.
Assignments
BFS: .
Ford Fulkerson: .
Edmonds Karp: .
Djikstra with min-heap: .
Prim’s algorithm:
Kruskal’s algorithm:
Bellman-Ford: .
ALGORITHMS
Recurrence Relations
Master method
Sorting Algorithms
Algorithms
Quickselect
Median Of Medians
Integer Multiplication
Convex Hull
Minimum Distance
0/1 Knapsack
Bellman Ford
Floyd Warshall
Fast Fourier Transform
++ Greedy Algorithm, Matroids
Hashing
Universal Hashing
Simple Uniform Hashing
Alpha Multiplication
Open Addressing
Compression
Fixed Length Coding
Prefix Free Coding
Hoffman Coding
NP Hardness