DMAT_L9

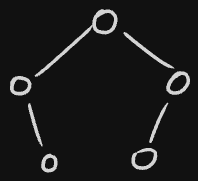
Catalan numbers

$C_n$ is the number of binary trees with $n$ nodes.
$(C_n)=(1,2,5,14,42,\dots )$.

Balanced strings

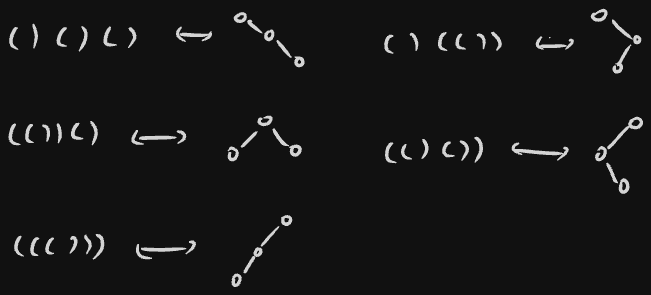
Consider all strings of length $2n$ over the alphabet $\{(,)\}$ that form balanced strings, i.e, the nesting of parenthesis is valid. For example, for $2n=4$, we have two: $()()$ and $(())$. For $2n=6$, we have 5: $()()()$, $((()))$, $(())()$, $()(())$, $(()())$. The number of such strings for $2n$ is equal to $C_n$.

A bijection between the set of all balanced strings of length $2n$ and the set of all binary trees on $n$ vertices

Given a balanced string, treat the interior of the first matched pair of parenthesis as the left child, and what follows as the right child. For example, in $(()())(())$, the left child is $()()$, and the right child is $(())$. It corresponds to this binary tree:

Here’s the bijection for $n=5$:

Monotonic lattice paths which do not pass over the diagonal

If we replace ’(’ with ‘R’ and ’)’ with ‘U’, then a balanced string of length $2n$ is a binary string with $n$ Rs and $n$ Us where each prefix has at least as many Rs as Us. If we now interpret the balanced string as a path in a $n\times n$ grid starting form the origin, the set of all balanced strings will represent the set of all monotonic paths from $(0,0)$ to $(n,n)$ which do not cross the $x=y$ line. These are the 14 paths for $n=4$:

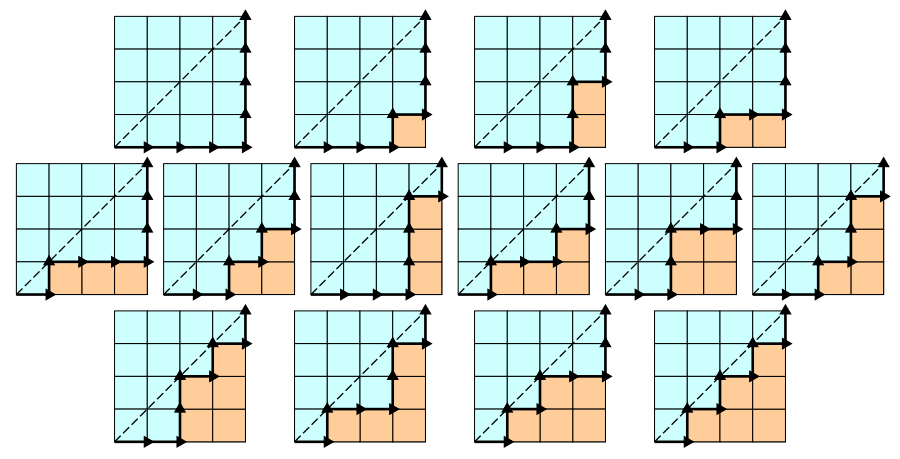
This manifestation of the Catalan numbers leads naturally to an explicit formula for $C_n$.

$$\begin{array}{rl}{C}_n=& (\text{number of paths from }(0,0)\text{ to }(n,n))-\\ & (\text{number of such paths which rise above the }x=y\text{ line})\end{array}$$

To compute the second term, notice that there exists a bijection between the set of all paths from $(0,0)$ to $(n,n)$ which rise above the $x=y$ line and the set of all paths from $(0,0)$ to $(n-1,n+1)$:

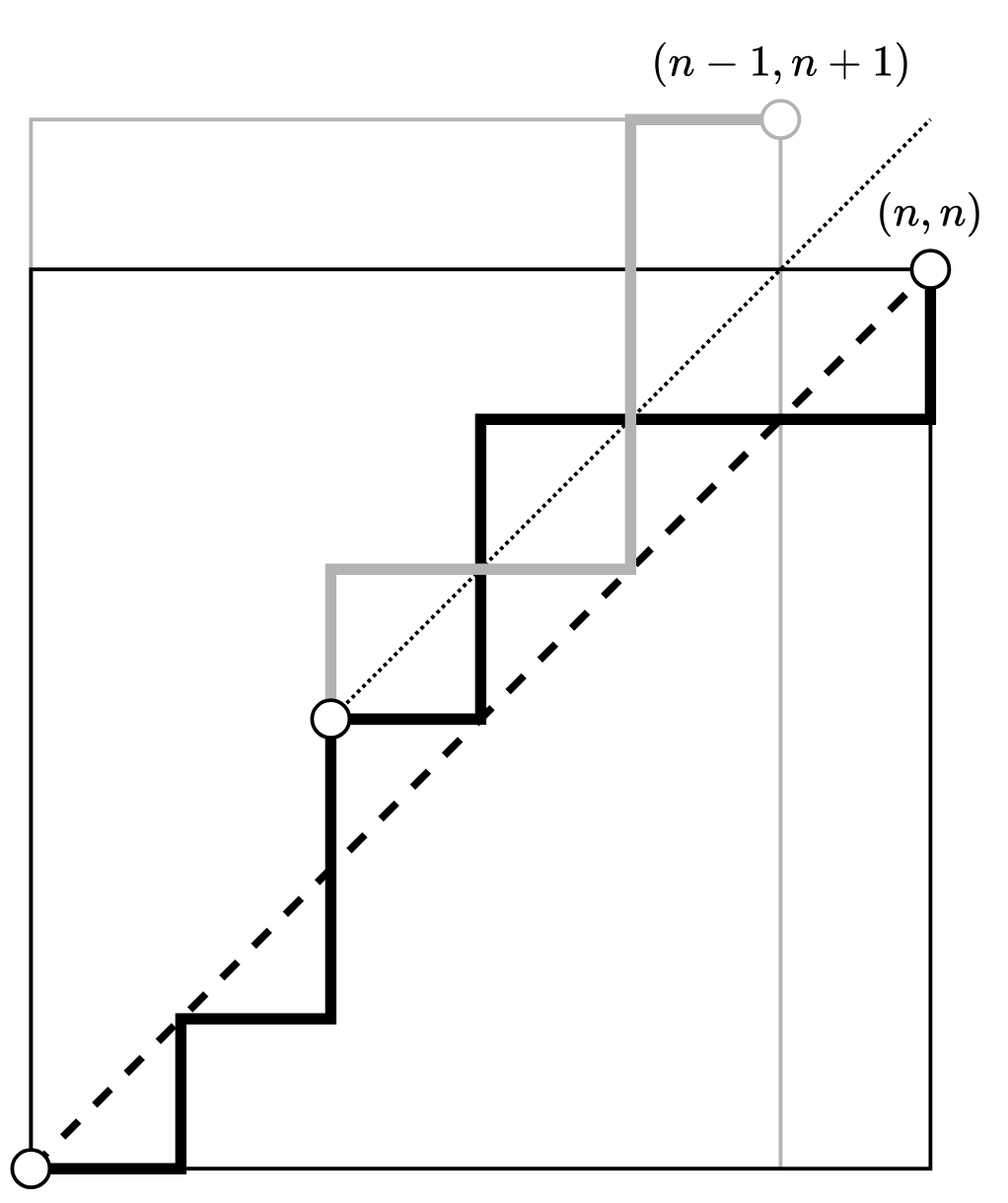
Thus, we have

$$C_n=\left(\genfrac{}{}{0ex}{}{2n}{n}\right)-\left(\genfrac{}{}{0ex}{}{2n}{n-1}\right).$$

The recurrence relation

$C_n$ has a non-linear recurrence, which should be evident from the binary trees perspective. To make things work, we take $C_0=1$.

$$C_n=\sum _{k=0}^{n-1}{C}_k{C}_{n-k-1}.$$

Let the generating function be

$$\varphi (x)=\sum _{n\ge 0}{C}_n{x}^n.$$

Now,

$$\begin{array}{rl}\varphi (x)& =\sum _{n\ge 1}\left(\sum _{k=0}^{n-1}{C}_k{C}_{n-k-1}\right)x^n+C_0\\ & =1+x\sum _{n\ge 0}\left(\sum _{k=0}^n{C}_k{C}_{n-k}\right)x^n\\ & =1+x\left(\sum _{i\ge 0}{C}_i{x}^i\right)\left(\sum _{j\ge 0}{C}_j{x}^j\right)\\ & =1+x\varphi (x{)}^2\end{array}$$

The roots are $\varphi (x)=\frac{1\pm \sqrt{1-4x}}{2x}$.

Note that in all our pervious encounters with generating functions, we got a single solution. The solution with the minus does not work, since it is not possible to associate a formal power series with it (trust me bro).

So, working with the other solution, we get

$$\begin{array}{rl}\varphi (x)& =\frac{1}{2x}(1-\sqrt{1-4x})\\ & =\frac{1}{-2x}\left(\sum _{n\ge 1}\left(\genfrac{}{}{0ex}{}{\frac{1}{2}}{n}\right)(-4x{)}^n\right)\\ & =2\sum _{n\ge 0}\left(\genfrac{}{}{0ex}{}{\frac{1}{2}}{n+1}\right)(-4x{)}^n\end{array}$$

(There is a truckload of justification that’s required for what we just did, but it’s ok to sweep it under the rug for now).

Finally, the Catalan numbers can be read off the coefficients:

$$\begin{array}{rl}{C}_n& =2\left(\genfrac{}{}{0ex}{}{\frac{1}{2}}{n+1}\right)(-4{)}^n\\ & =\cancel{2}\frac{\cancel{\left(\frac{1}{2}\right)}\left(\frac{1}{2}-1\right)\dots \left(\frac{1}{2}-n\right)}{(n+1)!}{4}^n(-1{)}^n\\ & =\frac{(2-1)(4-1)\dots (2n-1)}{(n+1)(n!)}{2}^n\\ & =\frac{1}{n+1}\left(\genfrac{}{}{0ex}{}{2n}{n}\right).\end{array}$$