DMAT_L24

Probabilistic methods in DM: Example 2

A hypergraph is made of hyperedges, which may connect more than two vertices.

A hypergraph is properly 2-colorable if its vertices can be assigned one of two colors (typically red and blue) in such a way that no hyperedge is entirely composed of vertices of the same color.

A hypergraph is k-uniform if every hyperedge has $k$ vertices.

Theorem 1(Theorem).

If $H$ is a $k$-uniform hypergraph with less than $2^{k-1}$ hyperedges, then $H$ is 2-colorable.

Proof
Color the vertices red or blue randomly uniformly independently. For every hyperedge $e$, let $A_e$ be the event that $e$ is monochromatic. $P(A_e)=2\cdot 2^{-k}=2^{1-k}$. Now,

$$\begin{array}{r}P\left(\bigcup _{e\in E(H)}{A}_e\right)\le \sum _{e\in E(H)}P(A_e)=|E(H)|2^{1-k}<1.\end{array}$$

Thus,

$$\begin{array}{r}P\left(\bigcap _{e\in E(H)}\overline{A_e}\right)=1-P\left(\bigcup _{e\in E(H)}{A}_e\right)>0.\end{array}$$

---

Planar graphs

Definition 2(Definition).

A planar graph is a graph which can be embedded into the plane such that no two edges cross each other. A specific embedding of a planar graph is called a plane graph.

$K_4$ is easily shown to be planar. $K_5$ and $K_{3,3}$ are famous examples of non-planar graphs.

Definition 3(Definition).

A region is an open set $U$ that contains a polygonal $u$-$v$ path for every $u,v\in U$.
The faces of a planar graph are maximal regions of the plane that are disjoint (when the planar graph is drawn without any crossings, of course).

The Jordan curve theorem says that any closed polygonal path divides the plane into two regions.

Some interesting results to prove:

• The double dual of a graph is isomorphic to itself iff the graph is connected.
• Every 3-connected planar graph has essentially one embedding.
• Every simple outer-planar graph has two non-adjacent vertices of degree at most 2.

Theorem 4(Euler's formula).

If a connected planar graph $G$ has $n$ vertices, $e$ edges, and $f$ faces, $n-e+f=2$.

Proof
By induction on $e$. If $e(G)=n-1$, then $G$ is a tree, and $f=1$. $n-e+f=2$. If $e(G)\ge n$, then $G$ contains a cycle $C$. Choose an edge $g$ in $C$ such that $G^{\prime }\equiv G\setminus g$ is connected. Then, $f^{\prime }=f-1$, $e^{\prime }=e-1$, and by induction hypothesis the theorem holds.

Euler’s theorem as stated fails for disconnected graphs. If a plane graph $G$ has $k$ components, then adding $k-1$ edges to $G$ yields a connected plane graph without changing the number of faces. Hence Euler’s Formula generalizes for graphs with $k$ components as $n-e+f=k+1$.

Definition 5(Definition).

The length of a face in a plane graph $G$ is the total length of the closed walk(s) in $G$ bounding the face.

A cut-edge belongs to the boundary of only one face, and it contributes twice to its length. For example, the embedding on the left has lengths 3, 6, 7; the one on the right has lengths 3, 4, 9:

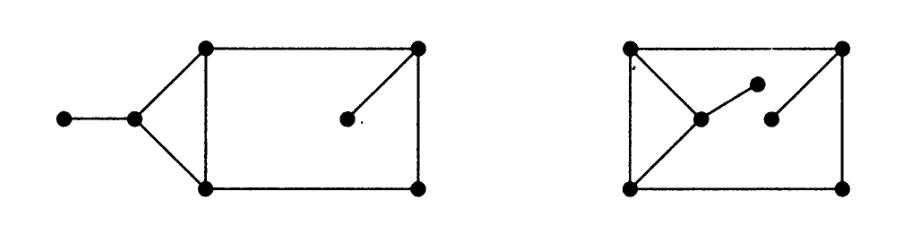
Both are embeddings of the same graph. So, different embeddings of the same graph might have different face lengths. However, there does exist an invariant quantity:

Theorem 6(Theorem).

In a plane graph $G$, $2e=\sum l(f_i)$.

Proof
Every edge in $G$ contributes twice to the sum on the right: if the edge is a cut edge, it contributes twice to the length of the same face, else it contributes once each to the two faces it bounds.

Since every embedding of a graph $G^{\prime }$ has the same value of $e$ as $G^{\prime }$, it follows that $\sum l(f_i)$ is the same for every embedding $G$ of $G^{\prime }$. Since $l(f_i)\ge 3$ for all faces, we have this corollary:

Theorem 7(Corollary).

In a plane graph $G$, $2e\ge 3f$.

Theorem 8(Corollary).

If $G$ is a simple planar graph with at least 3 vertices, then $e\le 3n-6$. Moreover, if $G$ is triangle free, then $e\le 2n-4$.

Proof
The first inequality is obtained by combining the previous corollary with Euler’s formula. If $G$ is triangle free, each face has length of at least four, so we have $2e\ge 4f$. Use Euler’s to get the second inequality.