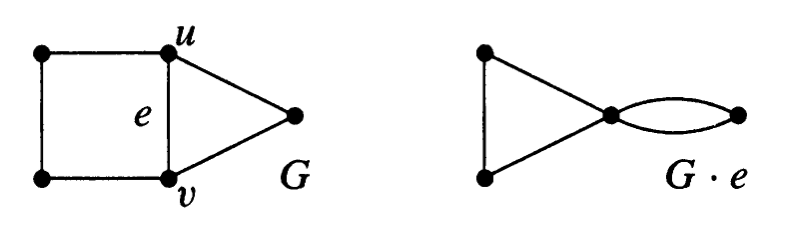DMAT_L18

Properties of trees

Theorem 1(Theorem).

For an $n$ vertex graph $G$, the following are equivalent (and characterize the trees with $n$ vertices).

1. $G$ is connected and has no cycles.
2. $G$ is connected and has $n-1$ edges.
3. $G$ has $n-1$ edges and no cycles.
4. For $u,v\in V(G)$, $G$ has exactly one $u,v$-path.

Theorem 2(Corollary).

1. Every edge of a tree is a cut-edge.
2. Adding one edge to a tree forms exactly one cycle.
3. Every connected graph contains a spanning tree.

Theorem 3(Theorem).

If $T,T^{\prime }$ are spanning trees of a connected graph $G$ and $e\in E(T)\setminus E(T^{\prime })$, then there is an edge $e^{\prime }\in E(T^{\prime })-E(T)$ such that

1. $T-e+e^{\prime }$ is a spanning tree of $G$, and
2. $T^{\prime }+e-e^{\prime }$ is a spanning tree of $G$.

Proof
Every edge of $T$ is a cut-edge of $T$. Let $U$ and $U^{\prime }$ be the two components of $T-e$. Let $E_1$ be the set of edges in $T^{\prime }$ with endpoints in $U$ and $U^{\prime }$. Since $T^{\prime }$ is connected, $E_1$ is nonempty.

Also, the graph $T^{\prime }+e$ contains a unique cycle $C$. Since $T$ is acyclic, $E_2\equiv E(C)\setminus E(T)$ is nonempty. Now, since $e\in E(C)$, and $e$ connects $U$ and $U^{\prime }$, there must be another edge $e^{\prime }\in E(C)$ which connects $U$ and $U^{\prime }$. Note that $e$ is the only edge in $T$ connecting $U$ and $U^{\prime }$. Thus, $e^{\prime }\in E_1\cap E_2$, and $T-e+e^{\prime }$ and $T^{\prime }+e-e^{\prime }$ are both spanning trees of $G$.

---

Spanning trees

Definition 4(Definition).

A spanning tree of a connected graph $G$ is a subgraph of $G$ which contains all the vertices of $G$, and is, of course, a tree.

Theorem 5(Theorem).

Every connected graph $G$ has a spanning tree.

Proof
Algorithmic constructive proof. Let $G=(V,E)$. $n$ vertices, $m$ edges. Let $E_0=\varnothing$, $V_0=\{v_0\}$, where $v_0$ is an arbitrary vertex. Having constructed $V_{i-1}$ and $E_{i-1}$ find an edge $e_i=\{x_i,y_i\}$ such that $x_i\in V_{i-1}$ and $y_i\in V\setminus V_{i-1}$. Then, $V_i=V_{i-1}\cup \{y_i\}$ and $E_i=E_{i-1}\cup \{e_i\}$. If no such edge exists, stop. If the algorithm returns $n-1$ edges, then the resulting subgraph is a spanning tree. Otherwise, $G$ is disconnected.

---

Counting spanning trees

ref

Given a graph $G$, we desire to count the number of spanning trees in $G$.

Definition 6(Definition).

In a graph $G$, contraction of edge $e$ with endpoints $u,v$ is the replacement of $u$ and $v$ with a single vertex whose incident edges are the edges other than $e$ that were incident to $u$ or $v$. The resulting graph $G\cdot e$ has one less edge than $G$.

Theorem 7(Lemma).

Let $\tau (G)$ denote the number of spanning trees of a graph $G$. If $e\in E(G)$ is not a loop, then $\tau (G)=\tau (G-e)+\tau (G\cdot e)$.

Theorem 8(Lemma).

If $G$ is a connected loopless graph with no cycle of length greater than 2, then $\tau (G)$ is the product of the edge multiplicities.

Graphs and matrices

Definition 9(Definition).

The adjacency matrix of a graph $G$ on $n$ nodes is the $n\times n$ matrix given by $\mathcal{A}=[a_{i,j}]$, where $a_{i,j}$ is the number of edges with endpoints $v_i$ and $v_j$.

If $G$ is loopless, all the diagonal entries of its adjacency matrix will be $0$.

Definition 10(Definition).

The Laplacian matrix of a graph $G$ on $n$ nodes is the $n\times n$ matrix $\mathcal{L}=\mathcal{D}-\mathcal{A}$, where $\mathcal{D}$ is the diagonal matrix $[d_{i,i}]$, $d_{i,i}=\text{degree}(v_i)$.

Note that each row sum/column sum of $\mathcal{L}$ is $0$.

Theorem 11(Lemma).

Let $G$ be a graph on $n$ nodes and $\mathcal{L}$ be its laplacian matrix. Then, $\det \mathcal{L}=0$.

Proof
Perform row operations ${\mathbf{r}}_1\to {\mathbf{r}}_1+{\mathbf{r}}_2+\cdots +{\mathbf{r}}_n$. Since each column sum is zero, this turns the first row into a zero row. It follows that the determinant must be zero.

$Q[i]$ denotes the matrix obtained on deleting the $i$th row and $i$th column from $Q$.

The following lemma should be clear:

Theorem 12(Lemma).

For any square matrix $A$, $\det (A+E_{ii})=\det (A)+\det A[i]$.

Matrix tree theorem

Theorem 13(Matrix tree theorem).

Given a loopless graph $G$ with vertex set $v_1,\dots ,v_n$, let $\mathcal{L}$ be its Laplacian matrix. If ${\mathcal{L}}^{\ast }$ is a matrix obtained by deleting row $s$ and column $t$ of $\mathcal{L}$, then $\tau (G)=(-1{)}^{s+t}\det {\mathcal{L}}^{\ast }$.

We will prove this for when $s=t$: $\tau (G)=\det \mathcal{L}[i]$ for any $i$.

Proof
If $G$ is not connected, let $v_i$ be an isolated vertex of $G$. Since the $i$th row and $i$th column of $\mathcal{L}$ are zero, $\mathcal{L}[i]$ retains the property of having zero row sum and column sum, and hence has determinant $0$. $\mathcal{L}[j]$ for $j\ne i$ would have a zero row, and hence have determinant zero. Checks out.

Now, let $G$ be connected. We induct on the number of edges of $G$. If $G$ has one edge, it must have exactly two vertices in order to not have loops and remain connected. The Laplacian matrix for $G$ would be

$$\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right].$$

Clearly, $\det \mathcal{L}[1]=\det \mathcal{L}[2]=1$, in agreement with the fact that $G$ has only one spanning tree.

Next, let $G$ have $k$ edges, and assume the theorem holds for all graphs with $k-1$ edges. Let $i\in [n]$, and let $e=\{v_i,v_j\}$ be an edge of $G$. Let ${\mathcal{L}}_{G-e}$ be the Laplacian matrix of $G-e$. Note that $\mathcal{L}[i]={\mathcal{L}}_{G-e}[i]+E_{j,j}$. So,

$$\begin{array}{rl}\det (\mathcal{L}[i])& =\det ({\mathcal{L}}_{G-e}[i]+E_{jj})\\ & =\det ({\mathcal{L}}_{G-e}[i])+\det ({\mathcal{L}}_{G-e}[i][j])\\ & =\det ({\mathcal{L}}_{G-e}[i])+\det (\mathcal{L}[i][j]).\end{array}$$

Depending on which vertex remains after a contraction, either ${\mathcal{L}}_{G\cdot e}[j]=\mathcal{L}[i][j]$ or ${\mathcal{L}}_{G\cdot e}[i]=\mathcal{L}[i][j]$. WLOG, assume the former. Note that both $G-e$ and $G\cdot e$ have one fewer edge than $G$.

$$\begin{array}{rl}\det (\mathcal{L}[i])& =\det ({\mathcal{L}}_{G-e}[i])+\det ({\mathcal{L}}_{G\cdot e}[j])\\ & =\tau (G-e)+\tau (G\cdot e)\\ & =\tau (G).\end{array}$$