ANA1_L29

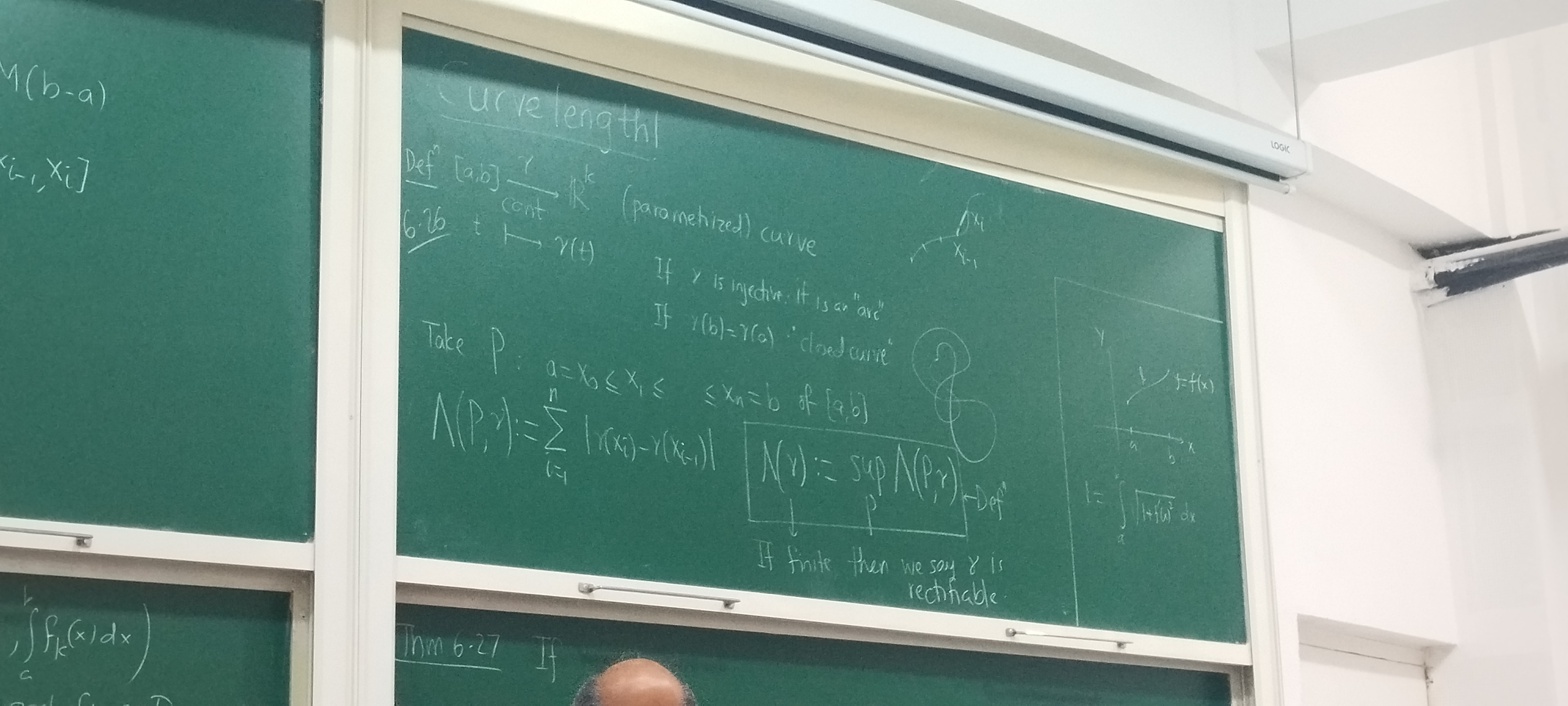
Integration of vector valued functions

Rudin, 6.23

Definition 1(Definition).

Let $f_1,f_2,\dots ,f_k:[a,b]\to \mathbb{R}$. Let $\mathbf{f}:[a,b]\to {\mathbb{R}}^k$ defined by $\mathbf{f}(x)=(f_1(x),f_2(x),\dots ,f_k(x))$.
We say $\mathbf{f}\in \mathcal{R}$ if $f_j\in \mathcal{R}$ for all $1\le j\le k$. If this is the case, we define

$${\int }_a^b\mathbf{f}dx=\left({\int }_a^b{f}_{1}dx,\dots ,{\int }_a^b{f}_{k}dx\right).$$

Similar definition exists for the Stieltjes integral. Note that parts a, c and e of the properties of integrals are valid for these integrals, and so is the fundamental theorem of calculus:

Rudin, 6.24

Theorem 2(Theorem).

Let $\mathbf{f}:[a,b]\to {\mathbb{R}}^k$. If $\mathbf{f}\in \mathcal{R}$ on $[a,b]$ and if there is a differentiable function $\mathbf{F}:[a,b]\to {\mathbb{R}}^k$ such that ${\mathbf{F}}^{\prime }=\mathbf{f}$, then

$${\int }_a^b\mathbf{f}(x)dx=\mathbf{F}(b)-\mathbf{F}(a).$$

Analogue of 6.13b

Rudin, 6.25

Theorem 3(Theorem).

Let $\mathbf{f}:[a,b]\to {\mathbb{R}}^k$. If $\mathbf{f}\in \mathcal{R}$, then

$$|\mathbf{f}|\in \mathcal{R}\text{ and }\left|{\int }_a^b\mathbf{f}dx\right|\le {\int }_a^b|\mathbf{f}|dx.$$

Proof
$|\mathbf{f}|=\sqrt{f_1^2+f_2^2+\dots f_k^2}$. By definition, each $f_i\in \mathcal{R}$. It follows that $f_i^2$ is integrable for each $i$, since $x^2$ is continuous (alternatively, the product of two integrable functions is integrable). Also, note that $x^2$ is bijective and continuous on $[0,\infty )$. Thus, $\sqrt{x}$ is continuous on $[0,\infty )$. It follows that $|\mathbf{f}|\in \mathcal{R}$.

Now, let $\mathbf{y}\equiv {\int }_a^b\mathbf{f}dx=(y_1,y_2,\dots ,y_n)$.

$$\begin{array}{rl}|\mathbf{y}{|}^2& =\sum _{j=1}^k{y}_j^2=\sum _{j=1}^k{y}_j\left({\int }_a^b{f}_{j}dx\right)={\int }_a^b\left(\sum _{j=1}^k{y}_j{f}_j\right)dx\\ & ={\int }_a^b\mathbf{y}\cdot \mathbf{f}dx.\end{array}$$

From the Cauchy-Schwarz inequality, we have

$$\mathbf{y}\cdot \mathbf{f}\le |\mathbf{y}||\mathbf{f}|.$$

Thus, we have

$$|\mathbf{y}{|}^2={\int }_a^b\mathbf{y}\cdot \mathbf{f}dx\le {\int }_a^b|\mathbf{y}||\mathbf{f}|dx=|\mathbf{y}|{\int }_a^b|\mathbf{f}|dx.$$

If $|\mathbf{y}|=0$, the result is trivial. If $|\mathbf{y}|\ne 0$, divide both sides by $|\mathbf{y}|$ to obtain the result. ❏

---

Rectifiable curves

Rudin, 6.26

Definition 4(Definition).

A continuous mapping $\mathbf{\gamma }:[a,b]\to {\mathbb{R}}^k$ is called a curve. If $\mathbf{\gamma }$ is injective, it is called an arc. If $\mathbf{\gamma }(b)=\mathbf{\gamma }(a)$, $\mathbf{\gamma }$ is called a closed curve.

Consider a partition $P=\{x_0,x_1,\dots ,x_n\}$ of $[a,b]$. Define

$$\begin{array}{r}\Lambda (P,\mathbf{\gamma })\equiv \sum _{i=1}^n|\mathbf{\gamma }(x_i)-\mathbf{\gamma }(x_{i-1})|;\end{array}$$ $$\Lambda (\mathbf{\gamma })\equiv \sup \Lambda (P,\mathbf{\gamma }).$$

If $\Lambda (\mathbf{\gamma })$ is finite, we say $\mathbf{\gamma }$ is rectifiable, and has length $\Lambda (\mathbf{\gamma })$.

To motivate what’s coming, let $f:[a,b]\to \mathbb{R}$ and let $\mathbf{\gamma }:[a,b]\to {\mathbb{R}}^2$, $x\stackrel{\mathbf{\gamma }}{\mapsto }(x,f(x))$ be the curve of $f$. Recall the high school formula for finding the length of the curve of $f$:

$$L={\int }_a^b\sqrt{1+f^{\prime }(x{)}^2}dx.$$

Note that ${\mathbf{\gamma }}^{\prime }(x)=(1,f^{\prime }(x))$, and that $L$ can be rewritten as

$${\int }_a^b|{\mathbf{\gamma }}^{\prime }(t)|dt.$$

Thus, it makes sense to conjecture that $\Lambda (\mathbf{\gamma })={\int }_a^b|{\mathbf{\gamma }}^{\prime }(t)|dt$ in general. For the integral to be defined, ${\mathbf{\gamma }}^{\prime }$ needs to exist, and $|{\mathbf{\gamma }}^{\prime }|$ needs to be integrable.
One way to ensure integrability is to require ${\mathbf{\gamma }}^{\prime }$ to be continuous, since that makes $|{\mathbf{\gamma }}^{\prime }|$ continuous, and continuous real valued functions are integrable.

Rudin, 6.27

Theorem 5(Theorem).

If ${\mathbf{\gamma }}^{\prime }$ exists and is continuous, then $\mathbf{\gamma }$ is rectifiable and

$$\Lambda (\mathbf{\gamma })={\int }_a^b|{\mathbf{\gamma }}^{\prime }(t)|dt.$$

Proof
Fix $P$. From the fundamental theorem of calculus and 6.25, we have

$$|\mathbf{\gamma }(x_i)-\mathbf{\gamma }(x_{i-1})|=\left|{\int }_{x_{i-1}}^{x_i}{\mathbf{\gamma }}^{\prime }(t)dt\right|\le {\int }_{x_{i-1}}^{x_i}|{\mathbf{\gamma }}^{\prime }(t)|dt.$$

Summing up both sides, we get

$$\Lambda (P,\mathbf{\gamma })\le {\int }_a^b|{\mathbf{\gamma }}^{\prime }(t)|dt.$$

Thus,

$$\Lambda (\mathbf{\gamma })=\sup \Lambda (P,\mathbf{\gamma })\le {\int }_a^b|{\mathbf{\gamma }}^{\prime }(t)|dt.$$

Now, if we bound the integral above by $\Lambda (\mathbf{\gamma })+ϵ$ where $ϵ$ is a quantity that can be made arbitrarily small, we are done. Let $ϵ>0$. Recall that since ${\mathbf{\gamma }}^{\prime }\in \mathcal{R}$ on $[a,b]$, ${\mathbf{\gamma }}^{\prime }$ is uniformly continuous on $[a,b]$. So, we get to pick $\delta >0$ such that whenever $|s-t|<\delta$, we have $|{\mathbf{\gamma }}^{\prime }(s)-{\mathbf{\gamma }}^{\prime }(t)|<ϵ$. Choose $P$ such that $\Delta x_i<\delta \forall i$. This ensures that for all $t\in [x_{i-1},x_i]$ we have ${\mathbf{\gamma }}^{\prime }(t)={\mathbf{\gamma }}^{\prime }(x_i)+\mathbf{\zeta }(t)$ where $|\mathbf{\zeta }(t)|<ϵ$. Now,

$$\begin{array}{rl}{\int }_{x_{i-1}}^{x_i}|{\mathbf{\gamma }}^{\prime }(t)|dt\le & {\int }_{x_{i-1}}^{x_i}|{\mathbf{\gamma }}^{\prime }(x_i)|dt+{\int }_{x_{i-1}}^{x_i}|\mathbf{\zeta }(t)|dt\\ =& \left|{\int }_{x_{i-1}}^{x_i}{\mathbf{\gamma }}^{\prime }(x_i)dt\right|+{\int }_{x_{i-1}}^{x_i}|\mathbf{\zeta }(t)|dt\\ \le & \left|{\int }_{x_{i-1}}^{x_i}{\mathbf{\gamma }}^{\prime }(x_i)dt\right|+ϵ\Delta x_i\\ =& \left|{\int }_{x_{i-1}}^{x_i}{\mathbf{\gamma }}^{\prime }(t)dt-{\int }_{x_{i-1}}^{x_i}\mathbf{\zeta }(t)dt\right|+ϵ\Delta x_i\\ \le & \left|{\int }_{x_{i-1}}^{x_i}{\mathbf{\gamma }}^{\prime }(t)dt\right|+\left|{\int }_{x_{i-1}}^{x_i}\mathbf{\zeta }(t)dt\right|+ϵ\Delta x_i\\ \le & |\mathbf{\gamma }(x_i)-\mathbf{\gamma }(x_{i-1})|+2ϵ\Delta x_i.\end{array}$$

Summing up both sides, we get

$$\begin{array}{rl}{\int }_a^b|{\mathbf{\gamma }}^{\prime }(t)|dt& \le \Lambda (P,\mathbf{\gamma })+2ϵ(b-a)\\ & \le \Lambda (\mathbf{\gamma })+2ϵ(b-a).\end{array}$$

This combined with the previous inequality gives

$$\Lambda (\mathbf{\gamma })\le {\int }_a^b|{\mathbf{\gamma }}^{\prime }(t)|dt\le \Lambda (\mathbf{\gamma })+2ϵ(b-a).$$

❏