Linear systems are solved by performing row reduction on the augmented matrix to reduce it to the echelon form, from which a solution can easily be written.
Echelon and reduced echelon form
Definition 275.1.
A matrix is in echelon form if it satisfies the following two conditions:
- All zero rows, if any, are below the non zero entries.
- For any non-zero row its leading entry(pivot) is strictly to the right of the leading entry in the previous row.
Definition 275.2.
A matrix is in reduced echelon form if it is in echelon form and
- All pivot entries equal 1
- All entries above the pivots are 0 (Note that all entries below the pivots are also zero cuz of echelon form).
Row operations
There are three row operations we can use to perform row reduction. Every row operation as what is called an elementary matrix associated with it, and performing the row operation is equivalent to multiplying the augmented matrix by the elementary matrix. Elementary matrices are invertible, and hence, performing row operations does not change the solution set of the system of linear equations (All solutions of the equation must satisfy , and any solution to the latter must satisfy ).
Row exchange
Let be the matrix
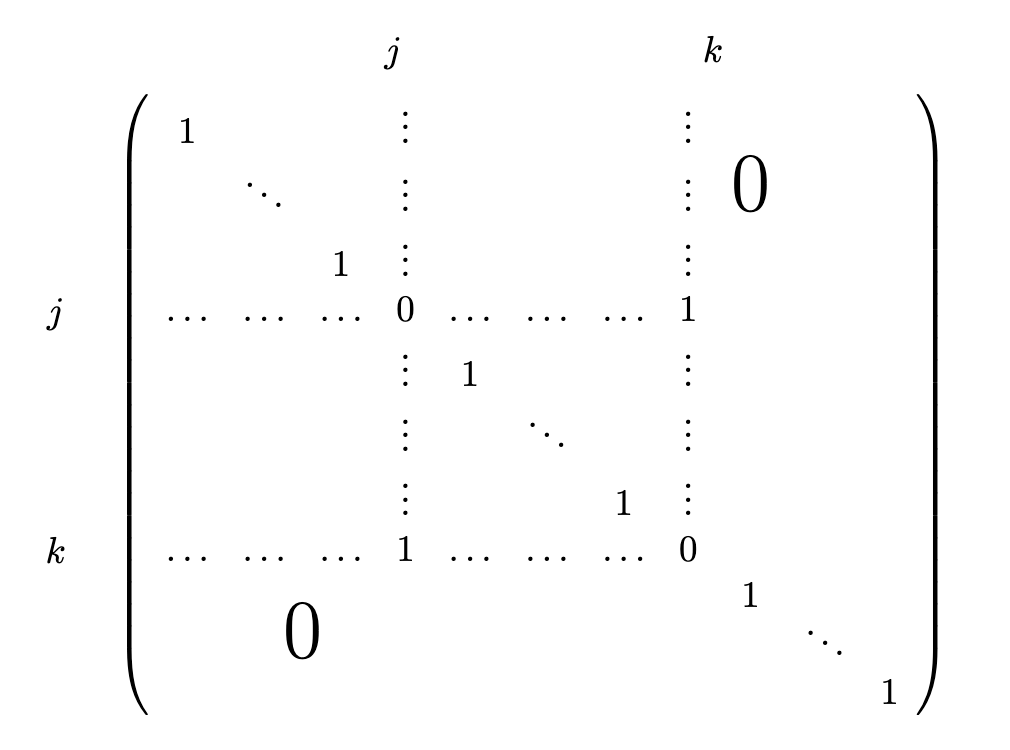
Then, rows and of are rows and of .
.
Row scaling
Let be the matrix

Then, row of is row of scaled by .
Replace by to obtain .
Row replacement
Let be the matrix

Then, row of is times row of added to row of .
Replace by to obtain .
Row reduction
Consists of three steps:
- Find the leftmost non-zero column of the matrix.
- Make sure, by applying row operations of type 1 (row exchange), if necessary, that the first (the upper) entry of this column is non-zero. This entry will be called the pivot entry or simply the pivot.
- “Kill” (i.e. make them 0) all non-zero entries below the pivot by adding (subtracting) an appropriate multiple of the first row from the rows number 2, 3, … , m.
- Forget the row you just worked with, and repeat from step 1 till you run out of rows or pivots.
The end result is a matrix in echelon form.
To get reduced echelon form from echelon form, we work from the bottom to the top and from the right to the left, using row replacement to kill all entries above the pivots.
The reduced echelon form of a matrix is unique. Proof.
Writing solution from RREF
Consider the RREF
Columns without a pivot are called free variables. The solution can be expressed in vector form like so:
Analyzing the pivots
All questions about existence of a solution and it uniqueness can be answered by analyzing pivots in the echelon (reduced echelon) form of the coefficient/augmented matrix.
Consider a linear system with equations and variables. It can be represented as , where is an matrix, , .
Analyzing the pivots in the coefficient matrix () tells us about the injectivity and surjectivity of the linear transformation represented by the coefficient matrix.
Important
- A solution for some (if it exists) is unique
there are no free variables
the echelon form has a pivot in every column.
the column vectors of are linearly independent- A solution exists for all
the echelon form of has no zero row
the echelon form of has a pivot in every row.
the column vectors of form a spanning set inIt follows from these statements that has a unique solution for every if and only if the echelon form of has a pivot in every column and row, i.e, the column vectors of are a basis in . Cf. Treil (2014, p. 57).
(*) and (**) are easy to see if you recall what matrix multiplication means, and what it means to be linearly independent/complete.
Given a vector in the codomain , analyzing the augmented matrix tells us whether the system is consistent for this choice of .
Important
A system is inconsistent for a given
there is a pivot in the last column of the echelon form of the augmented matrix.
Corollaries about linear independence and bases
Too hot
Theorem 275.3.
Any linearly independent system of vectors in cannot have more than vectors in it.
Proof
An matrix cannot have a pivot in every column if . ❏
Too cold
Theorem 275.4.
Any spanning set in must have at least vectors.
Proof
An matrix cannot have a pivot in every row if . ❏
Goldilocks?
Theorem 275.5.
Any basis in must have exactly vectors in it.
Proof
A basis must be linearly independent and complete. Thus, , and . ❏
Theorem 275.6.
Any two bases in a vector space have the same number of vectors in them.