Normalizers and Conjugacy

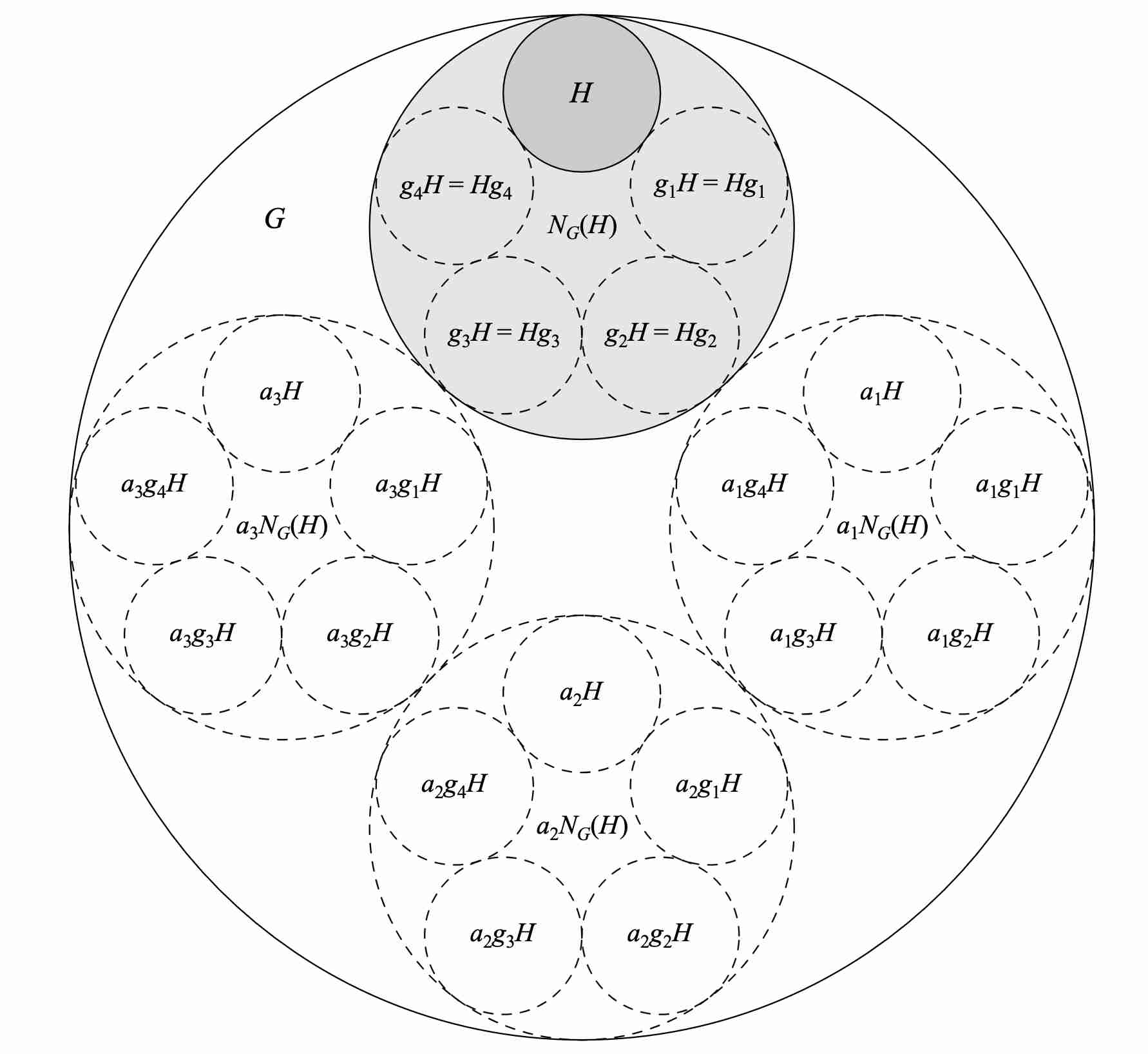
Is there a way to measure how close a subgroup is to being normal? We have said that a subgroup $H$ is normal when every element $g\in G$ satisfies $gH=Hg$. So a simple way to measure how close a subgroup is to normal is to check how many of the $g\in G$ satisfy this requirement. The set of $g\in G$ which satisfy $gH=Hg$ is called the normalizer of $H$ in $G$, denoted by $N_G(H)$.

• At minimum, we know that every $g\in H$ satisfies $gH=Hg$.
• Also note that cosets of $H$ vote together. If some $g\in G$ satisfies $gH=Hg$, all $g\in gH$ satisfy it. So, $N_G(H)$ is made up of whole cosets of $H$, and hence its size is a multiple of $|H|$.
• Furthermore, the deciding factor in how a left coset will vote is simply whether it is also a right coset. Thus, $N_G(H)$ is made up of all the left cosets that are also right cosets.

Example of a normalizer which is neither $H$ or $G$:

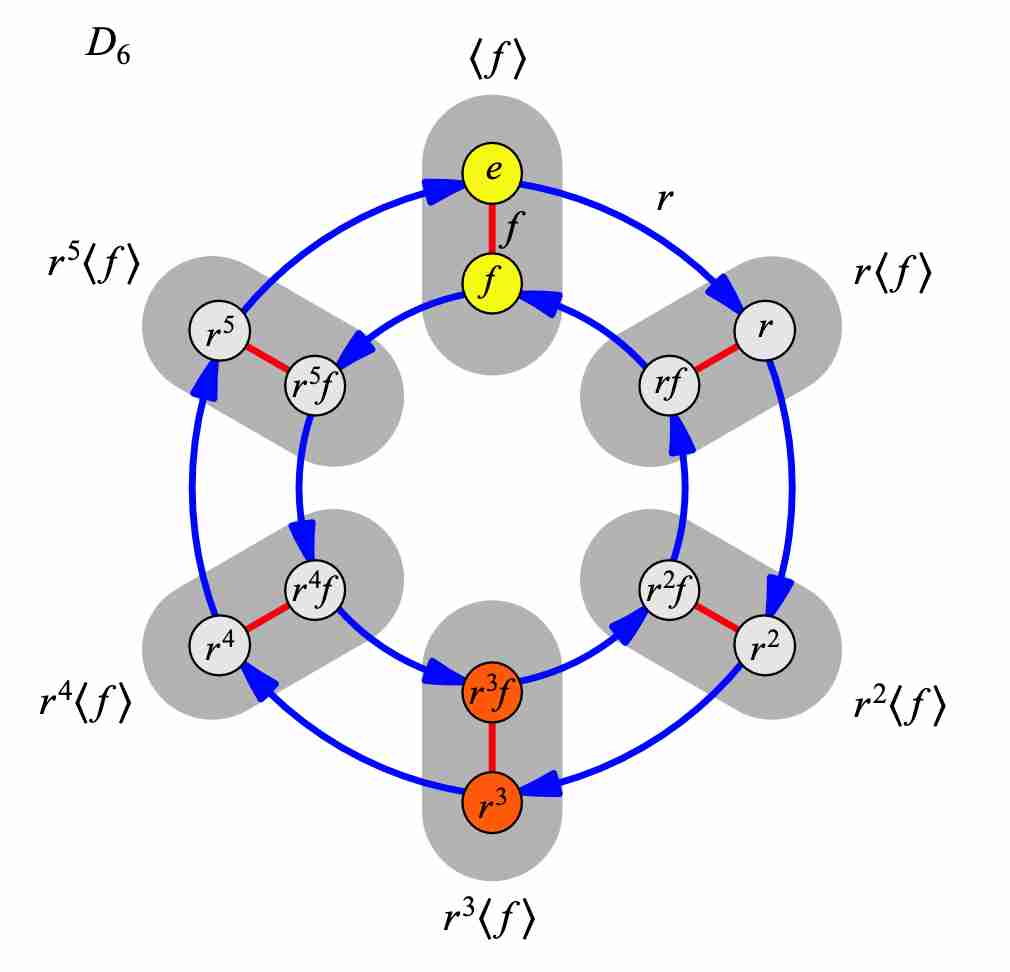
In $D_6$, the normalizer of $⟨f⟩$ is $\{e,f,r^{3}f,r^3\}$.

Theorem 1(Theorem).

For any $H<G$, $N_G(H)<G$. Furthermore, $H◃N_G(H)$.

Conjugacy

For $a\in G$, if $a=ba{b}^{-1}$ for some $b\in G$, $a$ and $b$ are said to be conjugates. Conjugacy is a equivalence relationship. Thus, we can partition a group into sets of conjugates, called conjugacy classes.

Conjugacy classes of $A_4$:

Elements	Description
$e$	identity
$(01)(23),(02)(13),(03)(12)$	180 degree flips
$(032),(123),(021),(301)$	120 degree clockwise rotations
$(012),(132),(230),(310)$	120 degree anti-clockwise rotations

Now, let $H$ be a normal subgroup, i.e, $gH{g}^{-1}=H$ for all $g\in G$. This means, for every $h\in H$, every element in $G$ that is conjugate to $h$ must be in $H$, its whole conjugacy class is in $H$. Thus, every normal subgroup is made up of whole conjugacy classes. This, in conjunction with the restrictions due to Lagrange’s theorem and inclusion of identity dramatically reduces the possibilities for normal subgroups.

Theorem 2(Lemma).

When a subgroup contains all of its conjugacy classes, it is a normal subgroup.