CM1 HW8

6.25

Let the line joining the pivot to the mass make an angle $\theta$ with the rod of length $l$.

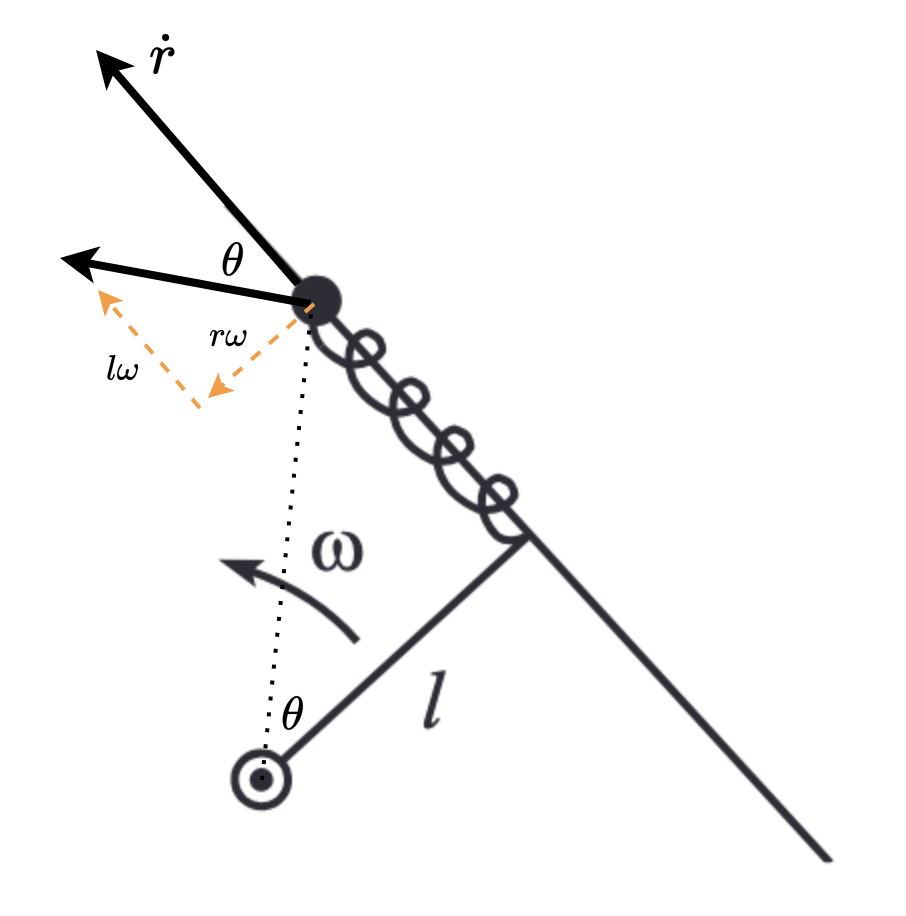
The components of the velocity of the mass along the rod and perpendicular to the rod will be $\dot{r}+l\omega$ and $-r\omega$ respectively. Thus, the kinetic energy of the mass is

$$T=\frac{1}{2}m((\dot{r}+l\omega {)}^2+(r\omega {)}^2)=\frac{1}{2}m({\dot{r}}^2+l^2{\omega }^2+2\dot{r}l\omega +r^2{\omega }^2).$$

Thus, the Lagrangian is

$$L=T-V=\frac{1}{2}m({\dot{r}}^2+l^2{\omega }^2+2\dot{r}l\omega +r^2{\omega }^2)-\frac{1}{2}k{r}^2.$$

The E-L equations yield

$$\begin{array}{rl}\frac{\partial L}{\partial r}& =\frac{d}{dt}\frac{\partial L}{\partial \dot{r}}\\ ⟹\ddot{r}& =r\left({\omega }^2-\frac{k}{m}\right).\end{array}$$

This linear differential equation describes different kinds of motion for different $\omega$:

$$\begin{array}{ll}{\omega }^2-\frac{k}{m}<0:& r\text{ performs oscillatory motion}\\ & r(t)=A\cos \left(t\sqrt{\frac{k}{m}-{\omega }^2}-\varphi \right)\\ {\omega }^2-\frac{k}{m}=0:& \dot{r}\text{ is constant}\\ & r(t)=At+C\\ {\omega }^2-\frac{k}{m}<0:& r\text{ increases exponentially}\\ & r(t)=A\cosh \left(t\sqrt{{\omega }^2-\frac{k}{m}}+\varphi \right)\end{array}$$

Thus, the special value of $\omega$ is $\sqrt{\frac{k}{m}}$, since this is the angular velocity at which the spring and centrifugal force exactly counteract each other.

---

6.33

From $6.19$, we have

$$\frac{\partial }{\partial a}S[x_a(t)]={\int }_{t_1}^{t_2}\left(\frac{\partial L}{\partial x_a}\beta +\frac{\partial L}{\partial {\dot{x}}_a}\dot{\beta }\right)dt.$$

Making copious use of the chain rule, we have

$$\begin{array}{rl}\frac{{\partial }^2}{\partial a^2}S[x_a(t)]& ={\int }_{t_1}^{t_2}\frac{\partial }{\partial a}\left(\frac{\partial L}{\partial x_a}\beta \right)+\frac{\partial }{\partial a}\left(\frac{\partial L}{\partial {\dot{x}}_a}\dot{\beta }\right)dt\\ & ={\int }_{t_1}^{t_2}\frac{\partial }{\partial a}\left(\frac{\partial L}{\partial x_a}\right)\beta +\frac{\partial }{\partial a}\left(\frac{\partial L}{\partial {\dot{x}}_a}\right)\dot{\beta }dt\\ & ={\int }_{t_1}^{t_2}\left(\frac{\partial }{\partial x_a}\left(\frac{\partial L}{\partial x_a}\right)\beta +\frac{\partial }{\partial {\dot{x}}_a}\left(\frac{\partial L}{\partial x_a}\right)\dot{\beta }\right)\beta \\ & +\left(\frac{\partial }{\partial x_a}\left(\frac{\partial L}{\partial {\dot{x}}_a}\right)\beta +\frac{\partial }{\partial {\dot{x}}_a}\left(\frac{\partial L}{\partial {\dot{x}}_a}\right)\dot{\beta }\right)\dot{\beta }dt\\ & ={\int }_{t_1}^{t_2}\frac{{\partial }^{2}L}{\partial x_a^2}{\beta }^2+2\frac{{\partial }^{2}L}{\partial x_a\partial {\dot{x}}_a}\beta \dot{\beta }+\frac{{\partial }^{2}L}{\partial {\dot{x}}_a^2}{\dot{\beta }}^{2}dt\end{array}$$

At $a=0$, $x_a=x$.

---

6.37

The constraint relation is

$$\eta =\sqrt{x^2+y^2}-R=0.$$

On differentiating twice, we get

$$\begin{array}{r}\frac{d}{dt}\eta =0⟹x\dot{x}+y\dot{y}=0\\ \frac{d}{dt}(x\dot{x}+y\dot{y})=0⟹{\dot{x}}^2+{\dot{y}}^2+x\ddot{x}+y\ddot{y}=0\end{array}$$

Plugging in the expressions for $\ddot{x}$ and $\ddot{y}$ in terms of $F$, we get

$$\begin{array}{r}{\dot{x}}^2+{\dot{y}}^2+\frac{F{x}^2}{mR}+\frac{F{y}^2}{mR}-gy=0\\ F=\frac{m}{R}(gy-\dot{x}-\dot{y})\end{array}$$

We now make the following substitutions:

$$\begin{array}{rl}& x=R\sin \theta \\ & y=R\cos \theta \\ & \dot{x}=R\cos \theta \dot{\theta }\\ & \dot{y}=-R\sin \theta \dot{\theta }\end{array}$$ $$\begin{array}{rl}F& =\frac{m}{R}(gR\cos \theta -R^2{\cos }^2\theta {\dot{\theta }}^2-R^2{\sin }^2\theta {\dot{\theta }}^2)\\ & =mg\cos \theta -mR{\dot{\theta }}^2\end{array}$$

Note

The second derivative supplied in the question is obtained on differentiating the first derivative before multiplying though by $\sqrt{x^2+y^2}$. I do not know why Morin prefers this, as the alternative yields a much cleaner equation to work with.

---

6.40

This system has two degrees of freedom. We will use $x$ and $y$ as our coordinates for the system. It is evident from the diagram that

$$\dot{z}=-\frac{\dot{x}+\dot{y}}{2}.$$

The Lagrangian is

$$\begin{array}{rl}L& =\frac{1}{2}4m{\left(\frac{\dot{x}+\dot{y}}{2}\right)}^2+\frac{1}{2}5m{\dot{x}}^2+\frac{1}{2}3m{\dot{y}}^2+4mg\left(\frac{x+y}{2}\right)-5mgx-3mgy+C,\end{array}$$

for some constant $C$. This simplifies to

$$\begin{array}{rl}L& =3m{\dot{x}}^2+2m{\dot{y}}^2+m\dot{x}\dot{y}-mg(3x+y).\end{array}$$

Consider the transformations

$$\begin{array}{rl}& x\mapsto x+ϵ\\ & y\mapsto y-3ϵ\end{array}$$

$\dot{x}$ and $\dot{y}$ are not affected by these transformations, and $3x-y$ remains unchanged under them. Thus, this transformation constitutes a symmetry of $L$, with $K_x=1$ and $K_y=-3$. It follows from Noether’s theorem that

$$\frac{\partial L}{\partial \dot{x}}{K}_x+\frac{\partial L}{\partial \dot{y}}{K}_y=m(3\dot{x}-11\dot{y})$$

is the corresponding conserved momentum.

---

6.45

Let $x$ be the position of the center of the ring, and let $\theta$ be the angle $m$ makes along the loop with the vertical. The velocity of $m$ in the ground frame will be

$$\begin{array}{rl}{v}_m^2& =(R\dot{\theta }+\dot{z}\cos \theta {)}^2+(\dot{z}\sin \theta {)}^2\\ & =R^2{\dot{\theta }}^2+{\dot{z}}^2+2R\dot{\theta }\dot{z}\cos \theta ,\end{array}$$

since the tangential velocity of the wheel does not affect the bead in any way. The Lagrangian of the system is

$$\begin{array}{rl}L& =\frac{1}{2}m(R^2{\dot{\theta }}^2+{\dot{z}}^2+2R\dot{\theta }\dot{z}\cos \theta )+\frac{1}{2}M{\dot{z}}^2+mg\cos \theta +C\end{array}$$

for some $C$. I’ve been unable to justify this, but applying the second order approximation $\cos \theta \approx 1$ for the first $\cos \theta$ term but not for the second gives us the coupled oscillator equations we are after:

$$\begin{array}{r}m{R}^2\ddot{\theta }+mR\ddot{z}=-mg\sin \theta \approx -mg\theta \\ \ddot{z}(m+M)=-Rm\ddot{\theta }\end{array}$$

Now, let the solution be of the form

$$\left[\begin{array}{c}\theta \\ z\end{array}\right]=\left[\begin{array}{c}A\\ B\end{array}\right]e^{i\alpha t}.$$

Then, the coupled equations can be represented in matrix form as

$$\left[\begin{array}{cc}g-R^2{\alpha }^2& -R{\alpha }^2\\ -Rm{\alpha }^2& -{\alpha }^2(m+M)\end{array}\right]\left[\begin{array}{c}A\\ B\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

Setting the determinant of the matrix to $0$ yields

$${\alpha }^2=0,\frac{g(m+M)}{M{R}^2}$$

If ${\alpha }^2=0$, the normal mode is $(0,1)$ ($A$ must be $0$, but $B$ is unrestricted).
If ${\alpha }^2=\frac{g(m+M)}{M{R}^2}$, the normal mode is $(m+M,-mR)$.
Thus, the solution is

$$\left[\begin{array}{c}\theta \\ z\end{array}\right]=A_1\left[\begin{array}{c}0\\ 1\end{array}\right](1+t)+A_2\left[\begin{array}{c}m+M\\ -mR\end{array}\right]\cos \left(t\sqrt{\frac{g(m+M)}{M{R}^2}}+\varphi \right).$$