CM1 HW7

7.7

Part a

The particle’s trajectory will be a standard hyperbola in a coordinate system where the axis and origin have been chosen appropriately, the equation of which will be

$$\begin{array}{r}\frac{1}{r}=\frac{m\alpha }{L^2}(1+ϵ\cos \theta ),\end{array}$$

where $\alpha =GmM$, $L=m{v}_{0}b$ and $ϵ=\sqrt{1+\frac{2E{L}^2}{m{\alpha }^2}}$, where $E=\frac{1}{2}m{v}_0^2$ (since the potential energy at $\infty$ is $0$). It is given that $ϵ>1$. So, the above equation can be rewritten as ($k\equiv \frac{L^2}{m\alpha }$)

$$\begin{array}{rl}& \frac{{\left(x-\frac{kϵ}{{ϵ}^2-1}\right)}^2}{a^2}-\frac{y^2}{b^2}=1.\\ \text{where }& a\equiv \frac{k}{{ϵ}^2-1}\text{ and }b\equiv \frac{k}{\sqrt{{ϵ}^2-1}}.\end{array}$$

We are given the distance of closest approach $b$, which is also the length of the semi-minor axis of the trajectory. $a$ can be computed with the given data:

$$\begin{array}{rl}a& =\frac{k}{{ϵ}^2-1}\\ & =\frac{km{\alpha }^2}{2E{L}^2}\\ & =\frac{L^{2}m{\alpha }^2}{m\alpha 2E{L}^2}\\ & =\frac{GM}{v_0^2}\end{array}$$

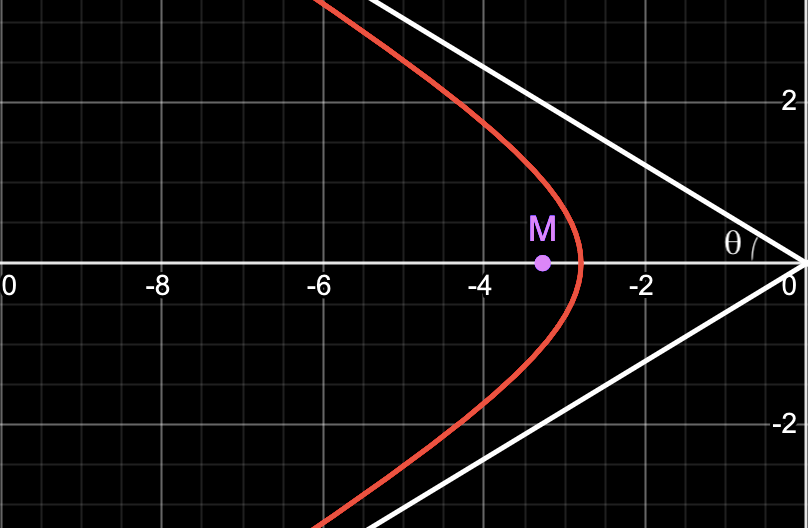
We know that the equations of the asymptotes of the hyperbola are $y=\pm \left(\frac{b}{a}\right)x$. Thus, $\theta ={\tan }^{-1}\left(\frac{b}{a}\right)={\tan }^{-1}\left(\frac{b{v}_0^2}{GM}\right)$. The angle of deflection, of course, is $\pi -2\theta =\pi -2{\tan }^{-1}\left(\frac{b{v}_0^2}{GM}\right)$, as desired.

Part b

Let $d\sigma$ be the area of the infinitesimal ring of inner radius $b$ and outer radius $b+db$. Then, $d\sigma =2\pi bdb$. We know from part $A$ that the angle of deflection is uniquely determined by the impact parameter $b$. Thus, all particles originating in this ring will have the same deflection angle $\varphi$.

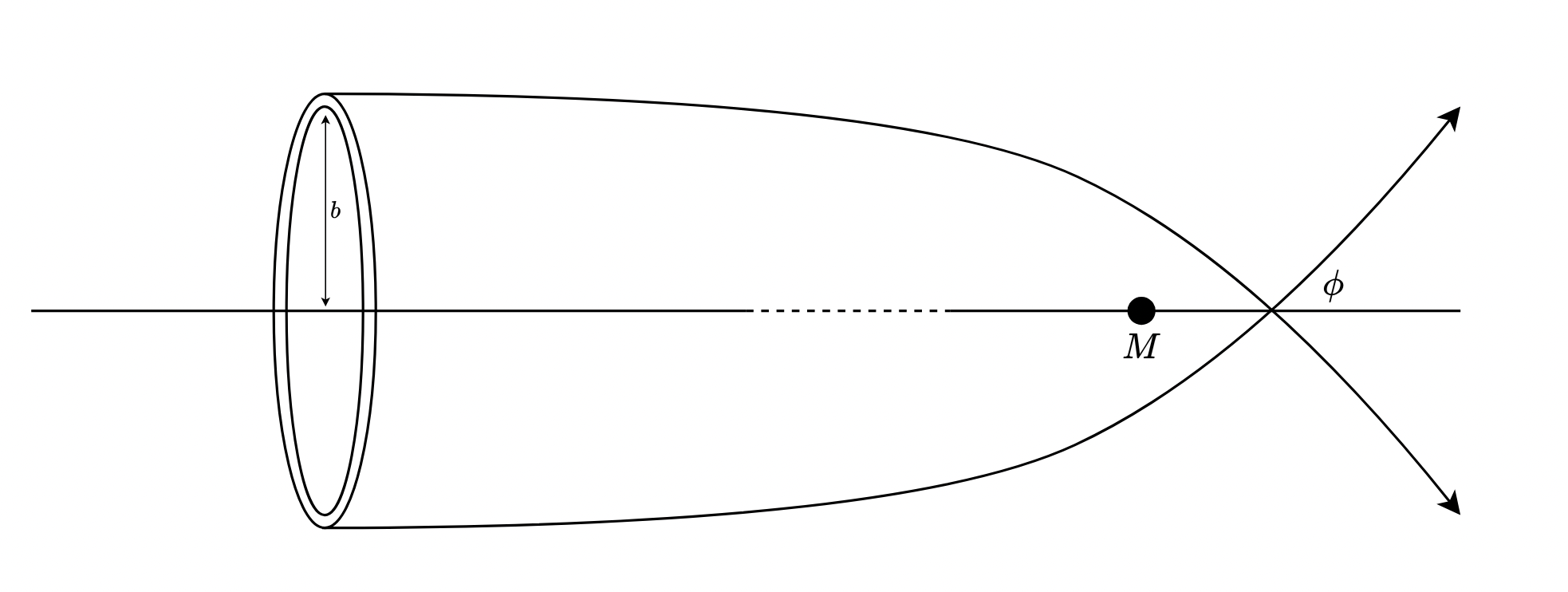
From part a, we have

$$\begin{array}{rl}& b=\frac{1}{\gamma }\cot \frac{\varphi }{2}\\ ⟹& \frac{db}{d\varphi }=-\frac{1}{\gamma }{\csc }^2\left(\frac{\varphi }{2}\right)\frac{1}{2}\end{array}$$

Also, we know that $\Omega =2\pi (1-\cos \varphi )$. It follows that $d\Omega =2\pi \sin \varphi d\varphi$. Now,

$$\begin{array}{rl}\frac{d\sigma }{d\Omega }& =\frac{bdb}{\sin \varphi d\varphi }\\ & =\frac{-1}{4{\gamma }^2{\sin }^4\frac{\varphi }{2}}\end{array}$$

---

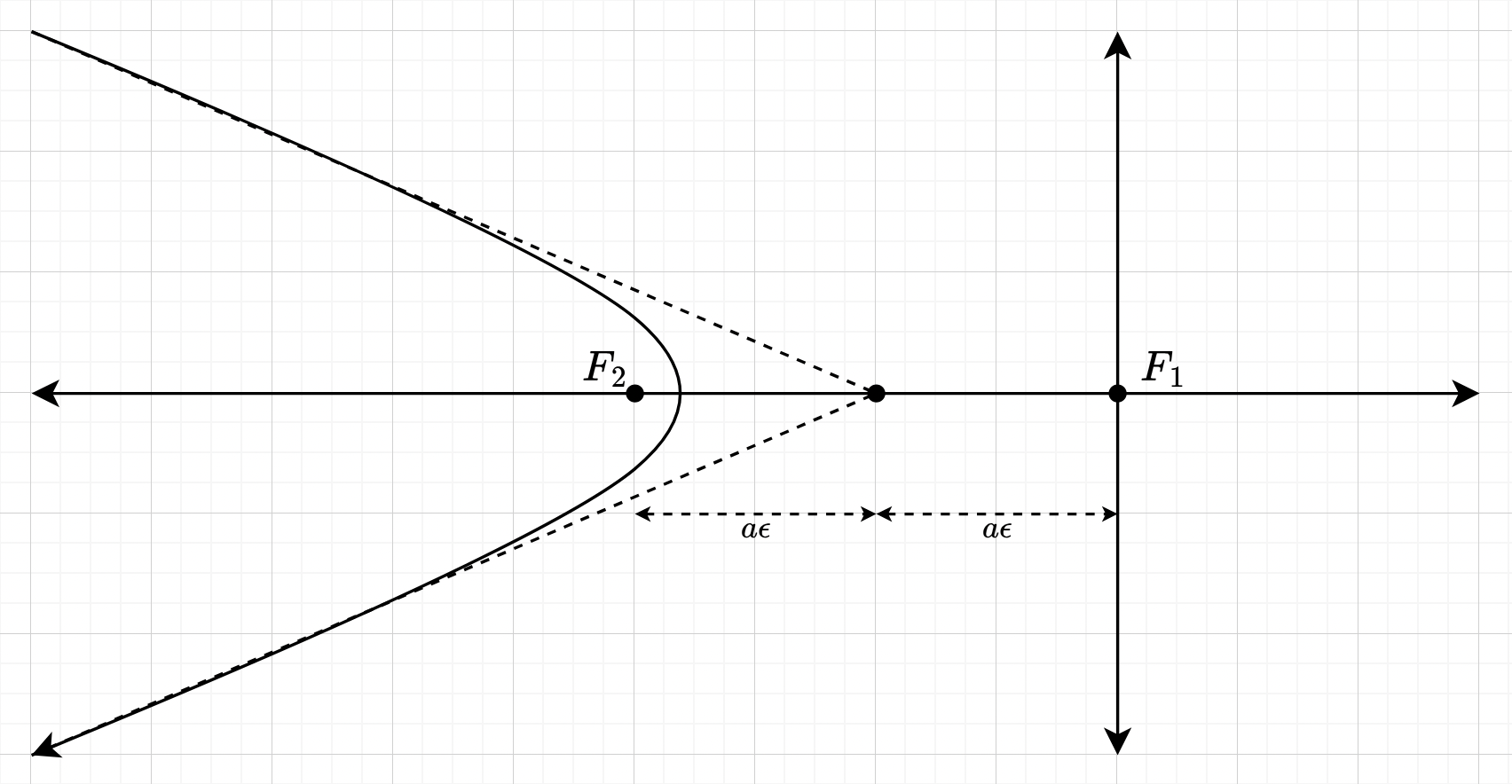
7.21

Redefining $V(r)$ to be $\frac{\alpha }{r}$ has the effect of replacing $\alpha$ with $-\alpha$ everywhere in section 7.4. Thus, for $r$ to be positive in

$$\begin{array}{r}\frac{1}{r}=\frac{m\alpha }{L^2}(1+ϵ\cos \theta ),\end{array}$$

$1+ϵ\cos \theta <0$, i.e, $ϵ$ must be greater than $1$ for the trajectory to be defined. Thus, only hyperbolic orbits can be achieved.

In the equation of the hyperbolic orbit given in 7.34, $k$ is now negative. Thus, the center of the hyperbola now lies at

$$\left(-\frac{kϵ}{{ϵ}^2-1},0\right).$$

The focus is $aϵ$ away from the center, the focii of the hyperbola are located at

$$\left(-\frac{2kϵ}{{ϵ}^2-1},0\right)\text{ and }(0,0).$$

$r$ is only defined when $-1\le \cos \theta <-\frac{1}{ϵ}$. Thus, the trajectory of the particle is the left branch of the hyperbola.