CM1 HW6

5.81

Let the two masses be $m_1$ and $m_2$, with $m_1$ moving to the right with a velocity ${\mathbf{u}}_1$ and $m_2$ stationary.

The position of the CM is given by ${\mathbf{r}}^{\prime }=\frac{m{\mathbf{r}}_1+m{\mathbf{r}}_2}{2m}=\frac{{\mathbf{r}}_1+{\mathbf{r}}_2}{2}$, where ${\mathbf{r}}_1$ and ${\mathbf{r}}_2$ are the positions of $m_1$ and $m_2$ with respect to the lab frame. The velocity of the CM is ${\mathbf{u}}^{\prime }=\frac{d{\mathbf{r}}^{\prime }}{dt}=\frac{{\mathbf{u}}_1}{2}$. It follows that ${\mathbf{u}}_1^{\prime }=\frac{{\mathbf{u}}_1}{2}$ and ${\mathbf{u}}_2^{\prime }=-\frac{{\mathbf{u}}_1}{2}$, where ${\mathbf{u}}_1^{\prime }$ and ${\mathbf{u}}_2^{\prime }$ are the velocities of $m_1$ and $m_2$ respectively in the CM frame.

Let the velocities of $m_1$ and $m_2$ after the collision be ${\mathbf{v}}_1^{\prime }$ and ${\mathbf{v}}_2^{\prime }$ in the CM frame. Say ${\mathbf{v}}_1^{\prime }$ makes an angle $\theta$ with the horizontal in the CM frame. Since the initial momentum was zero, it follows from the conservation of momentum that ${\mathbf{v}}_2^{\prime }$ must make an angle $\theta -\pi$ with the horizontal and have the same magnitude as ${\mathbf{v}}_1^{\prime }$. Thus, ${\mathbf{v}}_1^{\prime }=-{\mathbf{v}}_2^{\prime }\equiv {\mathbf{v}}^{\prime }$.

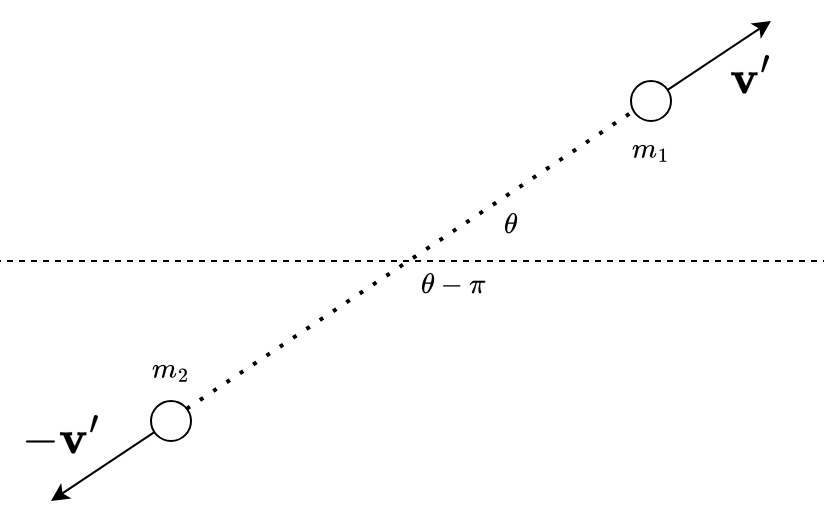
Angles are measured counterclockwise from the horizontal axis.

Also, since KE is conserved in the CM frame, $2\left(\frac{1}{2}m\frac{|{\mathbf{u}}_1{|}^2}{4}\right)=2\left(\frac{1}{2}m|{\mathbf{v}}^{\prime }{|}^2\right)$. So, $|{\mathbf{v}}^{\prime }|=\frac{|{\mathbf{u}}_1^{\prime }|}{2}$.

Let the final velocities of the masses in the lab frame be ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ respectively. We know that ${\mathbf{v}}_1={\mathbf{u}}^{\prime }+{\mathbf{v}}_1^{\prime }=\frac{{\mathbf{u}}_1}{2}+{\mathbf{v}}^{\prime }$ and ${\mathbf{v}}_2={\mathbf{u}}^{\prime }+{\mathbf{v}}_2^{\prime }=\frac{{\mathbf{u}}_1}{2}-{\mathbf{v}}^{\prime }$.

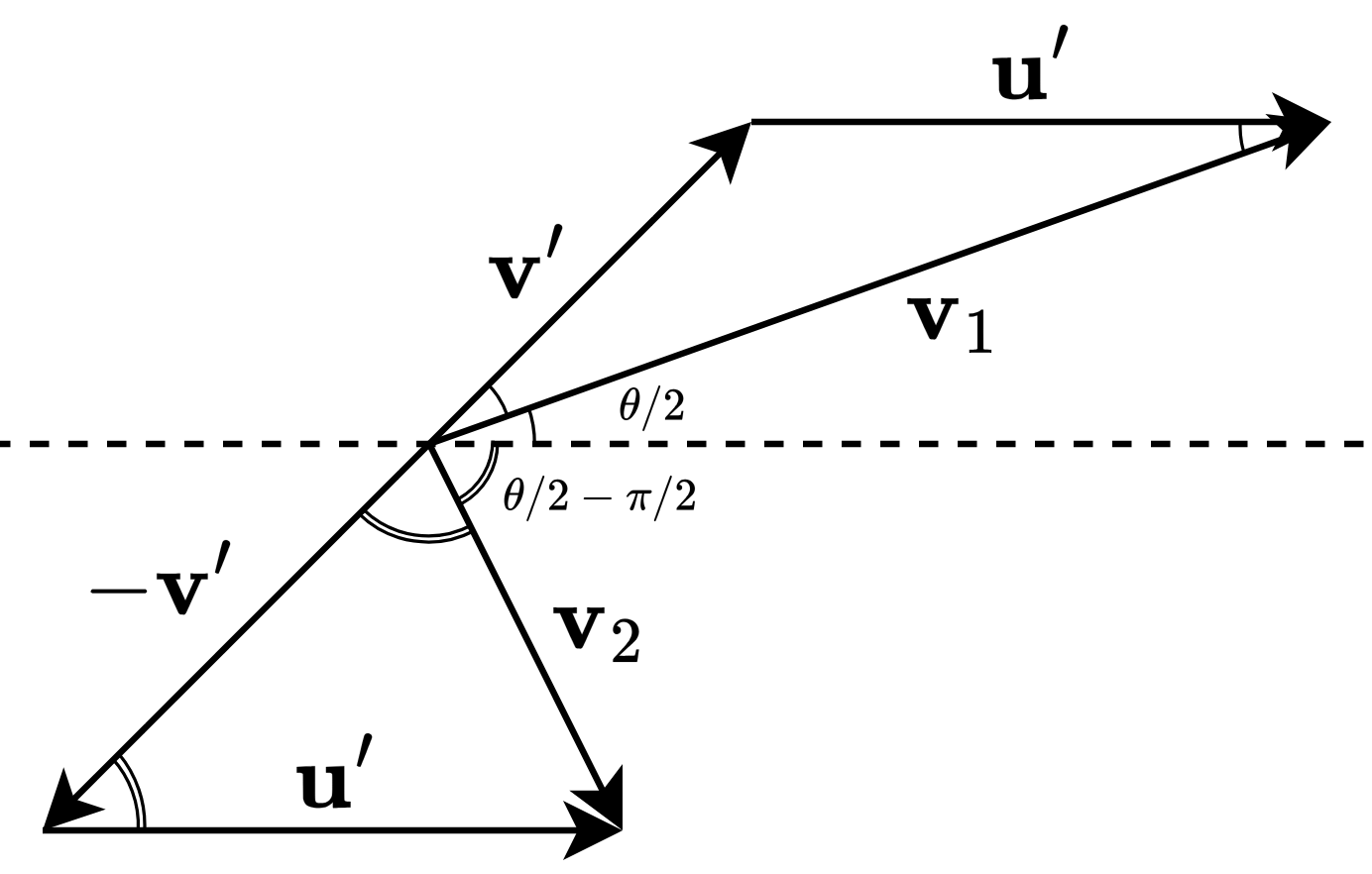
Elementary geometry tells us that ${\mathbf{v}}_1$ and ${\mathbf{v}}_2$ must be inclined at $\frac{\theta }{2}$ and $\frac{\theta }{2}-\frac{\pi }{2}$ to the horizontal axis. Hence, they are perpendicular. The magnitudes of the final velocities can be obtained using the law of cosines.

$$\begin{array}{r}|{\mathbf{v}}_1|=\sqrt{\frac{|{\mathbf{u}}_1{|}^2}{4}+\frac{|{\mathbf{u}}_1{|}^2}{4}+\frac{|{\mathbf{u}}_1{|}^2}{2}\cos \theta }=\frac{|{\mathbf{u}}_1|}{2}\sqrt{2+2\cos \theta }=|{\mathbf{u}}_1|\cos \frac{\theta }{2}\\ |{\mathbf{v}}_2|=|{\mathbf{u}}_1|\sin \frac{\theta }{2}\end{array}$$

---

5.91

Consider the system at an arbitrary time $t$, when the chain is not completely extended. Since the heap is in free fall, it has fallen by a distance $\frac{1}{2}g{t}^2$. The force applied at the top end can be expressed as the sum of the force required to hold this $\frac{1}{2}g{t}^2$ length of chain at rest ($F_1$), and the force required to induce the change in momentum experienced by the part of the chain which comes to rest during a time interval $dt$ ($F_2$).

The first part of the force, $F_1=(\text{mass of still chain})g=\left(\frac{1}{2}g{t}^2\sigma \right)g$.

To find the second part of the force, we must find the change in momentum of the piece of chain that comes to rest in $dt$. The finial momentum is $0$. The initial momentum is $dmv=(\sigma |v|dt)(v)=-\sigma (gt{)}^{2}dt$. Thus,

$$F_2=\frac{dp}{dt}=\frac{0-(-\sigma (gt{)}^{2}dt)}{dt}=\sigma (gt{)}^2$$

So,

$$F=F_1+F_2=\frac{1}{2}\sigma (gt{)}^2+\sigma (gt{)}^2=\frac{3}{2}\sigma (gt{)}^2.$$

Now, the chain will unravel completely when $\frac{1}{2}g{t}^2=L⟹t=\sqrt{\frac{2L}{g}}$. So, for $t\ge \sqrt{\frac{2L}{g}}$, $F_2=0$, and $F_1$ becomes constant at $L\sigma g$. Thus, we have

$$F=\{\begin{array}{ll}\frac{3}{2}\sigma (gt{)}^2& t<\sqrt{\frac{2L}{g}}\\ L\sigma g& t\ge \sqrt{\frac{2L}{g}}\end{array}.$$