CM1 HW5

5.49

By conserving total energy between the bob being released and the string being cut, we can compute the velocity of the bob when the string is cut.

$$\begin{array}{rl}\left(\frac{1}{2}m{v}^2-0\right)+(-mgl\cos \theta -0)& =0\\ v& =\sqrt{2gl\cos \theta }.\end{array}$$

If the string makes an angle $\theta$ with the vertical, the bob’s velocity makes an angle $\theta$ with the horizontal. We can apply a standard result from projectile motion to obtain the range of the bob from the point where the string is cut:

$$R=\frac{u^2\sin 2\theta }{g}=2l\cos \theta \sin 2\theta$$

To maximize $R$, we find its critical points.

$$\begin{array}{rl}\frac{dR}{d\theta }& =-2l\sin \theta \sin 2\theta +4l\cos \theta \cos 2\theta =0\\ ⟹& (2\cos \theta \cos 2\theta -\sin \theta \sin 2\theta )=0\end{array}$$

On solving for $\theta$, we get $\theta ={\sin }^{-1}\left(\frac{1}{\sqrt{3}}\right)$.

---

5.61

Part a

Gauss’s law of gravitation states that

$${\int }_S\mathbf{E}\cdot d\mathbf{A}=-4\pi Gm,$$

Where $S$ is a closed surface, $\mathbf{E}$ is the gravitational field, and $M$ is the total mass enclosed within the surface. Since the mass distribution is symmetrical about the center of the shell and $\mathbf{E}$ and $d\mathbf{A}$ are always in the same direction, if we take $S$ to be a sphere concentric with the shell, the above formula can be reduced to

$$E{\int }_{S}dA=-4\pi Gm,$$

where $E=|\mathbf{E}|$ and $dA=|d\mathbf{A}|$.
We can now divide the problem into three parts.

$r<R_1$

Since $S$ not enclose any mass, $m=0$.

$$E\cdot {\int }_{S}dA=0⟹E=0\text{ at every point on S.}$$

Thus, for $r<R_1$, $E=0$.

$R_1<r<R_2$

$S$ will now enclose some mass $m$:

$$m=M\left(\frac{r^3-R_1^3}{R_2^3-R_1^3}\right).$$

So, we have

$$\begin{array}{rl}E\cdot {\int }_{S}dA=E(4\pi r^2)& =-4\pi GM\left(\frac{r^3-R_1^3}{R_2^3-R_1^3}\right)\\ ⟹E& =-\frac{GM}{r^2}\left(\frac{r^3-R_1^3}{R_2^3-R_1^3}\right)\end{array}.$$

Since $\mathbf{E}$ is always in the radial direction, we can cast the above relation in vector form:

$$\mathbf{E}=\frac{GM}{r^2}\left(\frac{r^3-R_1^3}{R_2^3-R_1^3}\right)(-\hat{\mathbf{r}})$$

$R_2<r$

$S$ will now enclose all of the shell’s mass.

$$\begin{array}{r}E{\int }_{S}dA=-4\pi GM\\ ⟹E=-\frac{GM}{r^2}\\ ⟹\mathbf{E}=\frac{GM}{r^2}(-\hat{\mathbf{r}}).\end{array}$$

---

From $\mathbf{F}=m\mathbf{E}$, we have

$$\begin{array}{r}\mathbf{F}(\mathbf{r})=\{\begin{array}{ll}0& |\mathbf{r}|<R_1\\ \frac{GMm}{|\mathbf{r}{|}^2}\left(\frac{|\mathbf{r}{|}^3-R_1^3}{R_2^3-R_1^3}\right)(-\hat{\mathbf{r}})& R_1<|\mathbf{r}|<R_2\\ \frac{GMm}{|\mathbf{r}{|}^2}(-\hat{\mathbf{r}})& R_2<|\mathbf{r}|\end{array}\end{array}$$

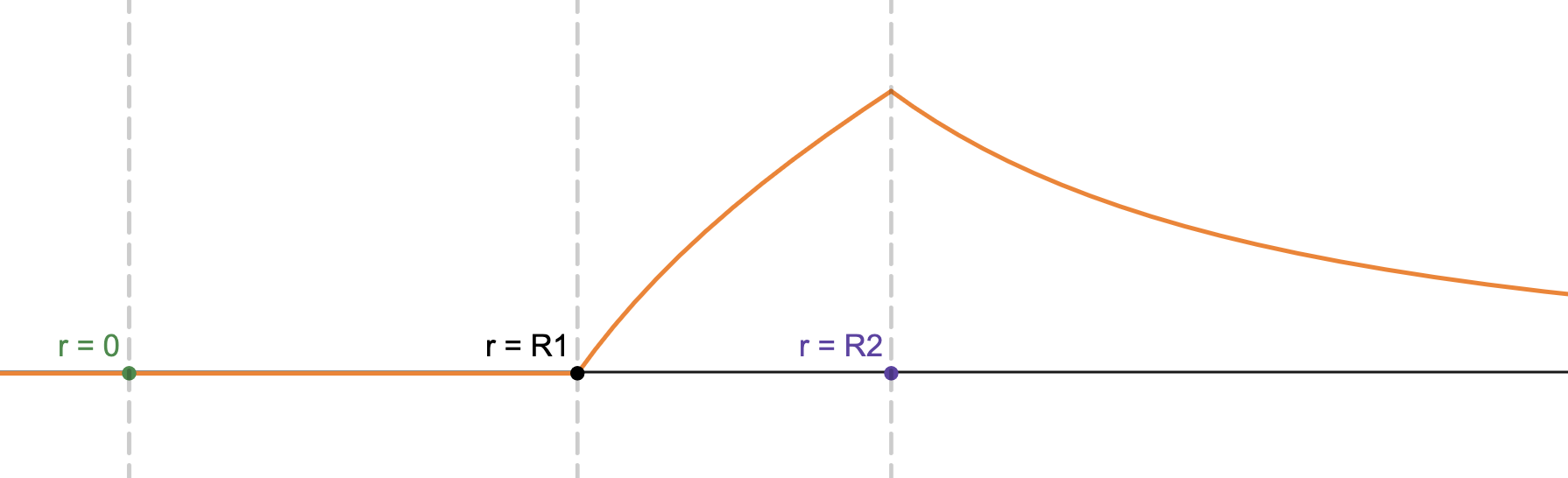
A rough sketch, with $|\mathbf{F}(\mathbf{r})|$ on the y-axis and $|\mathbf{r}|$ on the x-axis.

Part b

Since no external force acts on the mass $m$ during the course of its journey, we can conserve total mechanical energy, i.e, $\Delta K=-\Delta U$, where $\Delta K$ is the change in kinetic energy and $\Delta U$ is the change in potential energy.

$$\begin{array}{rl}\Delta V=V(0)-V(\infty )& ={\int }_0^{\infty }\mathbf{E}\cdot d\mathbf{r}\\ & ={\int }_0^{R_1}\mathbf{E}\cdot d\mathbf{r}+{\int }_{R_1}^{R_2}\mathbf{E}\cdot d\mathbf{r}+{\int }_{R_2}^{\infty }\mathbf{E}\cdot d\mathbf{r}\\ & =-{\int }_0^{R_1}0dr-{\int }_{R_1}^{R_2}\frac{GM}{r^2}\left(\frac{r^3-R_1^3}{R_2^3-R_1^3}\right)dr-{\int }_{R_2}^{\infty }\left(\frac{GM}{r^2}\right)dr\\ & =0-\frac{GM\left(R_2-R_1\right)\left(R_2+2R_1\right)}{2R_2\left(R_2^2+R_1{R}_2+R_1^2\right)}-\frac{GM}{R_2}\\ & =-\frac{3GM}{2}\left(\frac{R_2+R_1}{R_2^2+R_1{R}_2+R_1^2}\right)\end{array}.$$

In the third step, The fact that $\mathbf{E}\cdot d\mathbf{r}=|\mathbf{E}||d\mathbf{r}|\cos \pi$ has been used.
From energy conservation, we have

$$\begin{array}{rl}\Delta K=\frac{1}{2}m{v}^2-0& =-\Delta U=-m\Delta V=\frac{3GMm}{2}\left(\frac{R_2+R_1}{R_2^2+R_1{R}_2+R_1^2}\right)\\ ⟹v& =\sqrt{3GM\left(\frac{R_2+R_1}{R_2^2+R_1{R}_2+R_1^2}\right)}\end{array}$$

On plugging in $R_2=2R_1=R$, we get

$$v=\sqrt{\frac{9}{7}\frac{GM}{R}}$$

---

5.63

Let the tube be at a distance $d$ away from the center of the Earth. Denote the distance of the object from the middle point of the tube by $x$. When the object is at a distance $r$ from the center of the Earth, the gravitational force acting on it can be calculated using the equations derived in the previous problem after plugging $R_1=0$, and $R_2={\mathrm{R}}_e$, and $M=\frac{4}{3}\pi R_e^3\rho$

$$\mathbf{F}=\frac{GMmr}{R_e^3}=\frac{4}{3}\pi \rho Gmr(-\hat{\mathbf{r}})$$

Since we can only concerned about the component of force along the tube, we can replace $r$ with its projection on the tube, $x$.

$$\begin{array}{r}{F}_x=-\frac{4\pi \rho Gm}{3}x\\ ⟹a=-\frac{4\pi \rho G}{3}x\end{array}$$

Thus, the object performs SHM. Its angular frequency is given by

$$\omega =\sqrt{\frac{4\pi \rho G}{3}}.$$

The time period, $T=\frac{2\pi }{\omega }$, is approximately $84.5\text{ minutes}$. So, the object would take nearly 42 minutes to reach the other end.