CM1 HW4

4.23

Part a

Let $x$ be the arc length traversed by the bob, i.e, $x=l\theta$.

$$\begin{array}{rlr}T=4{\int }_0^{T/4}dt& =4{\int }_0^{{\theta }_{0}l}\frac{1}{v}dx=4l{\int }_0^{{\theta }_0}\frac{1}{v}d\theta & (1)\end{array}$$

From the second law equation for the pendulum bob, we have $-mg\sin \theta =ma⟹a=-g\sin \theta$. Since $a=v\frac{dv}{dx}$, we have $vdv=-g\sin \theta dx$.

$$\begin{array}{rl}vdv& =-gl\sin \theta d\theta \\ \int vdv& =-gl\int \sin \theta d\theta +c\\ v^2& =2gl\cos \theta +c^{\prime }\end{array}$$

When $\theta ={\theta }_0$, $v=0$. Thus, $c^{\prime }=-2gl\cos {\theta }_0$. This gives us an expression for $v$ in $\theta$, $v=\sqrt{2gl(\cos \theta -\cos {\theta }_0)}$, which we can plug into $(1)$ to obtain the desired expression for $T$.

$$\begin{array}{rlr}T& =\sqrt{\frac{8l}{g}}{\int }_0^{{\theta }_0}\frac{1}{\sqrt{\cos \theta -\cos {\theta }_0}}d\theta & (2)\end{array}$$

Part b

On using the suggested trigonometric identity in $(2)$, we get

$$\begin{array}{rl}T& =2\sqrt{\frac{l}{g}}{\int }_0^{{\theta }_0}\frac{1}{\sqrt{{\sin }^2({\theta }_0/2)-{\sin }^2(\theta /2)}}d\theta \\ & =2\sqrt{\frac{l}{g{\sin }^2({\theta }_0/2)}}{\int }_0^{{\theta }_0}\frac{1}{\sqrt{1-{\left(\sin (\theta /2)/\sin ({\theta }_0/2)\right)}^2}}d\theta .\end{array}$$

Making the suggested substitution of $\sin x\equiv \frac{\sin \left(\frac{\theta }{2}\right)}{\sin \left(\frac{{\theta }_0}{2}\right)}$ (note that this $x$ is different from the $x$ used in part $(a)$), we get

$$\begin{array}{r}T=4\sqrt{\frac{l}{g}}{\int }_0^{\pi /2}\frac{1}{\cos \frac{\theta }{2}}dx=4\sqrt{\frac{l}{g}}{\int }_0^{\pi /2}{\left(1-{\sin }^{2}x{\sin }^2\frac{{\theta }_0}{2}\right)}^{-1/2}dx.\end{array}$$

The Maclaurin series for $\sin x$ is $x-\frac{x^3}{3!}+\frac{x^5}{5!}+\dots$ . Since we are only interested in an approximation up to the second order of ${\theta }_0$, we can approximate ${\sin }^2\frac{{\theta }_0}{2}\approx \frac{{\theta }_0^2}{4}$.

We can now employ the Maclaurin series of the function $f(y)=(1+y{)}^{\alpha }$:

$$\begin{array}{r}(1+y{)}^{\alpha }=1+\alpha y+\frac{1}{2}\alpha (\alpha -1)y^2+\dots .\end{array}$$

On plugging $y=-{\sin }^{2}x\left(\frac{{\theta }_0^2}{4}\right)$ and $\alpha =-\frac{1}{2}$, and approximating $(1+y{)}^{\alpha }\approx 1+\alpha y$ (since we only require the first power of $y$ to obtain an approximation in ${\theta }_0^2$), we get

$$\begin{array}{rl}T& \approx 4\sqrt{\frac{l}{g}}{\int }_0^{\pi /2}1+\frac{1}{2}{\sin }^{2}x\frac{{\theta }_0^2}{4}+\dots dx\\ & =4\sqrt{\frac{l}{g}}{\left(x+\frac{{\theta }_0^2}{8}\left(\frac{x}{2}-\frac{\sin 2x}{4}\right)+\dots \right)}_0^{\pi /2}\\ & =4\sqrt{\frac{l}{g}}\left(\frac{\pi }{2}+\frac{{\theta }_0^2}{8}\left(\frac{\pi }{4}\right)+\dots \right)\\ & =2\pi \sqrt{\frac{l}{g}}\left(1+\frac{{\theta }_0^2}{16}+\dots \right),\end{array}$$

as desired.

---

4.33

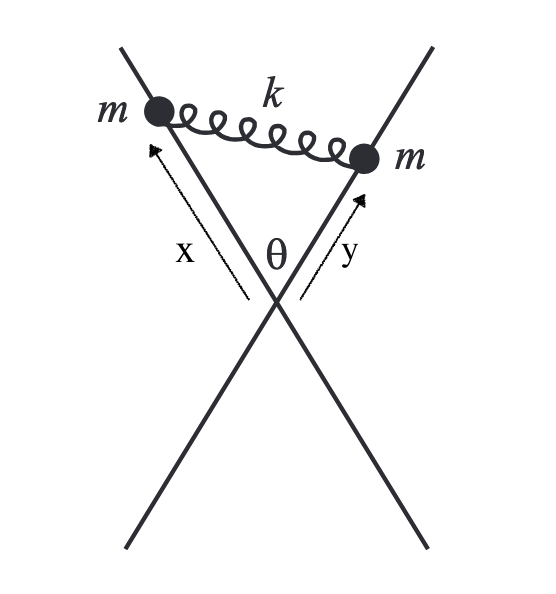
Let the two masses be $m_1$ and $m_2$, and their distances from the origin (where the two rails cross each other) are $x$ and $y$ respectively. We can write the second law equations for both beads only considering the component of the spring force along their rails, as the perpendicular component is nullified by normal forces.

$$\begin{array}{rlr}{m}_1& :k(y\cos \theta -x)=m\ddot{x}& (1)\\ m_2& :k(x\cos \theta -y)=m\ddot{y}& (2)\end{array}$$

Adding $(1)$ and $(2)$, we obtain

$$\begin{array}{rlr}& (\ddot{x}+\ddot{y})+(x+y)(1-\cos \theta )\frac{k}{m}=0& \\ ⟹& x+y=A\cos \left(t\sqrt{(1-\cos \theta )\frac{k}{m}}+{\varphi }_1\right)& (3)\end{array}$$

for some constants $A$ and ${\varphi }_1$. Similarly, on subtracting $(2)$ from $(1)$, we obtain

$$\begin{array}{rlr}& (\ddot{x}-\ddot{y})+(x-y)(1+\cos \theta )\frac{k}{m}=0& \\ ⟹& x-y=B\cos \left(t\sqrt{(1+\cos \theta )\frac{k}{m}}+{\varphi }_2\right)& (4)\end{array}$$

for some constants $B$ and ${\varphi }_2$. Thus, $x+y$ and $x-y$ are the normal modes, as they oscillate with pure frequencies. $(3)$ and $(4)$ can be solved for $x(t)$ and $y(t)$.

$$\begin{array}{r}x=\frac{A}{2}\cos \left(t\sqrt{(1-\cos \theta )\frac{k}{m}}+{\varphi }_1\right)+\frac{B}{2}\cos \left(t\sqrt{(1+\cos \theta )\frac{k}{m}}+{\varphi }_2\right)\\ y=\frac{A}{2}\cos \left(t\sqrt{(1-\cos \theta )\frac{k}{m}}+{\varphi }_1\right)-\frac{B}{2}\cos \left(t\sqrt{(1+\cos \theta )\frac{k}{m}}+{\varphi }_2\right)\end{array}$$