CM1 HW2

3.30

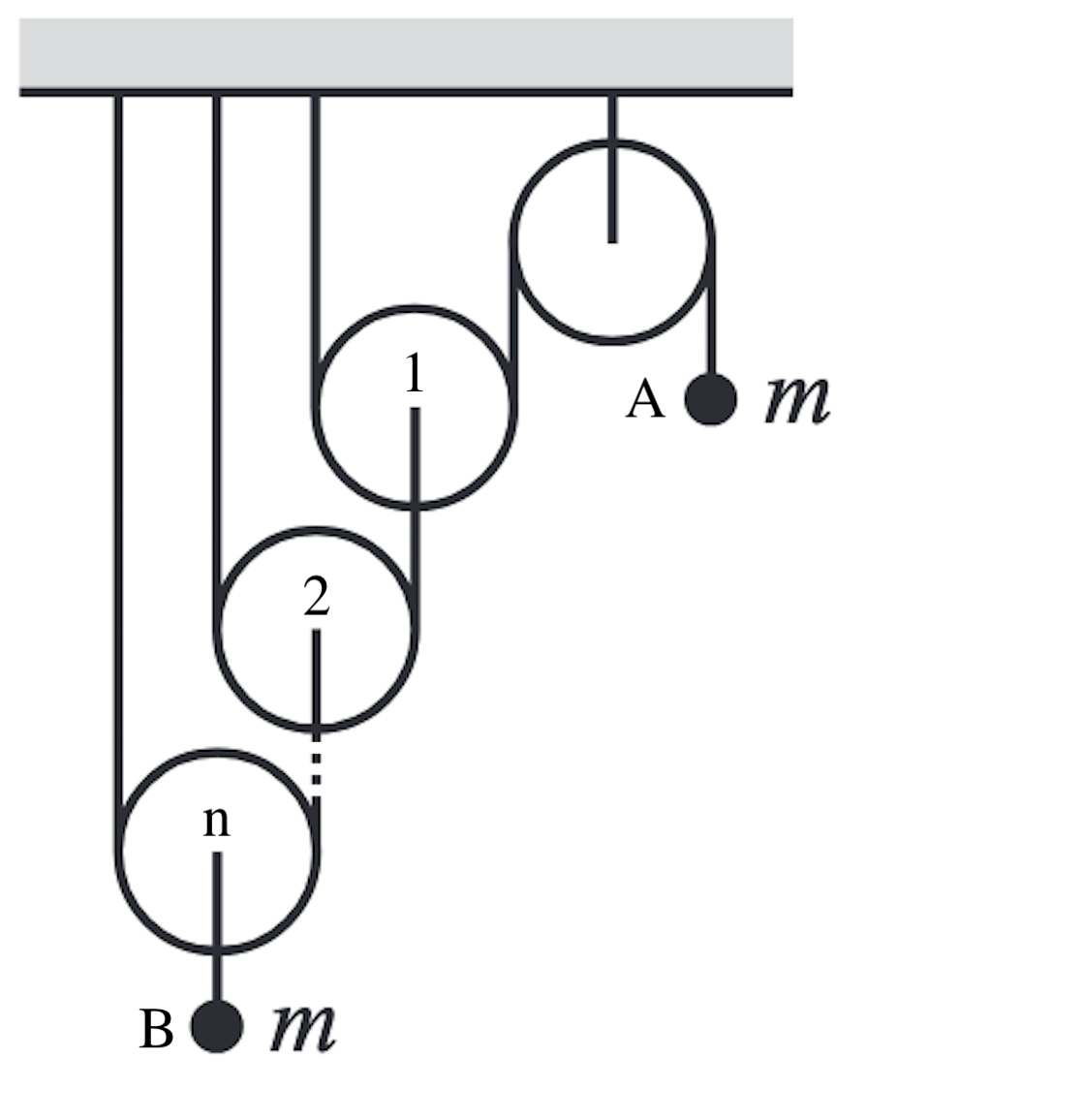
Let $A$ have acceleration $a$ and tension $T$ acting upward. Then, from the conservation of string, pulley 1 must have upward acceleration of $\frac{a}{2}$, pulley 2 $\frac{a}{4}$, and pulley $n$ (and hence $B$) $\frac{a}{2^n}$. Similarly, if $A$ experiences an upward tension of $T$, pulley 1 must experience a total upward tension of $2T$, pulley 2 $4T$, and pulley $n$ (and hence $B$) $2^{n}T$.

We can now proceed to write the second law equations for both the blocks.

$$\begin{array}{rl}\text{block A: }& T-mg=-ma\\ \text{block B: }& 2^{n}T-mg=m\frac{a}{2^n}\end{array}$$

Solving these equations for $a$, we get

$$\boxed{a=\frac{g(2^n-1)}{2^{-n}+2^n}}$$

3.44

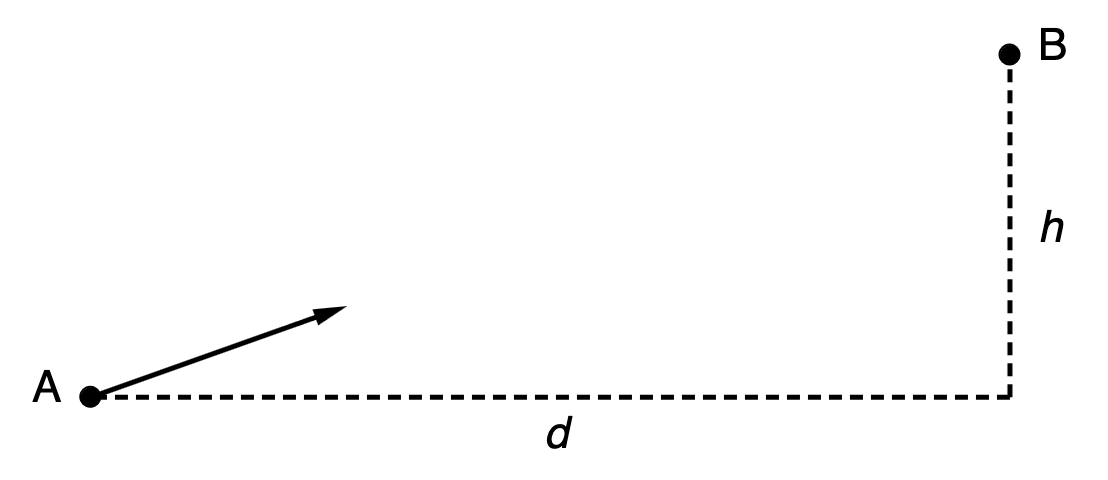
Suppose Newton is at $A(0,0)$, and he aims his rock at an apple located at $B(d,h)$ with a velocity $\mathbf{v}$. Let ${\mathbf{r}}_1$ denote the position of the rock, and ${\mathbf{r}}_2$ denote the position of the apple. ${\mathbf{r}}_1$ and ${\mathbf{r}}_2$ can be parameterized in $t$ like so (let $\theta =\arctan \left(\frac{h}{d}\right)$):

$$\begin{array}{rl}{\mathbf{r}}_1& =\left(|\mathbf{v}|\cos \theta t,|\mathbf{v}|\sin \theta t-\frac{1}{2}g{t}^2\right),\\ {\mathbf{r}}_2& =\left(d,h-\frac{1}{2}g{t}^2\right)\end{array}$$

Equating the $\text{x}$ coordinates, we get $t=\frac{d}{|\mathbf{v}|\cos \theta }$, the time at which the rock and apple will have the same $\text{x}$ coordinate. On plugging this value of $t$ into the expressions for ${\mathbf{r}}_1$ and ${\mathbf{r}}_2$, we get

$$\boxed{\begin{array}{r}{\mathbf{r}}_1={\mathbf{r}}_2=\left(d,h-\frac{g{d}^2}{2|\mathbf{v}{|}^2{\cos }^2\theta }\right)\end{array}}$$

Thus, the rock hits the apple.

3.57

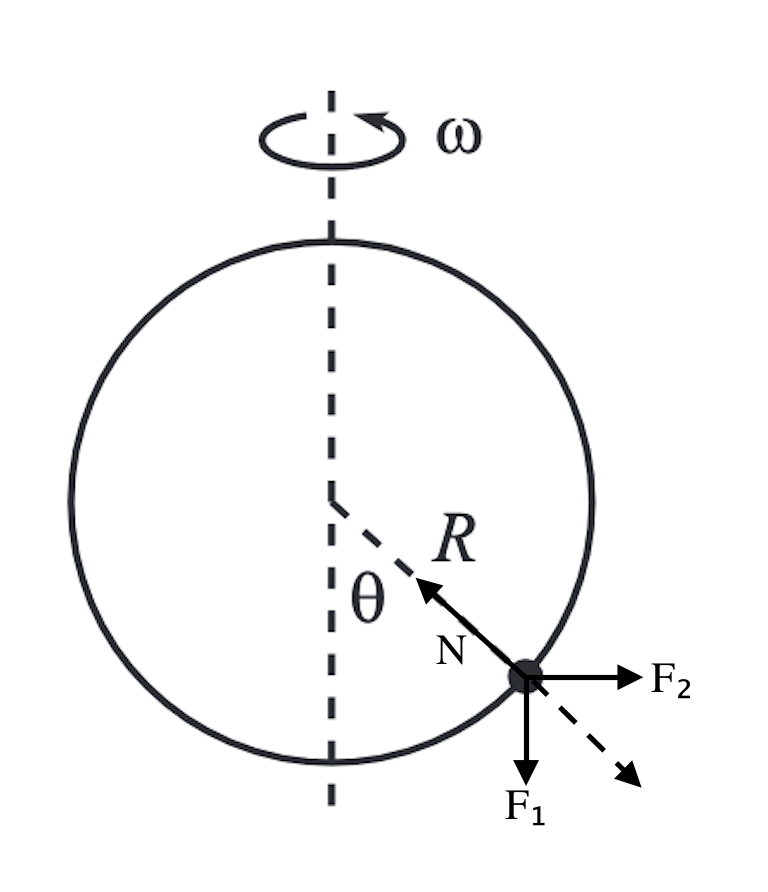
From the frame of reference of the hoop, the bead will experience a fictitious force ${\mathbf{F}}_2=mR\sin \theta {\omega }^2\hat{r}$, gravitational force ${\mathbf{F}}_1=-mg\hat{k}$, and normal force due to the hoop $\mathbf{N}$. For the bead to remain at the same angle $\theta$ relative to the vertical, the resultant of ${\mathbf{F}}_1$ and ${\mathbf{F}}_2$ must be antiparallel to $\mathbf{N}$. Thus,

$$\begin{array}{rl}& \frac{|{\mathbf{F}}_2|}{|{\mathbf{F}}_1|}=\tan \theta \\ ⟹& \frac{R\sin \theta {\omega }^2}{g}=\tan \theta \\ ⟹& \boxed{\omega =\sqrt{\frac{g}{R\cos \theta }}}\end{array}$$

When $\theta =0$, $\omega =\sqrt{\frac{g}{R}}$. This implies that if $\omega \le \sqrt{\frac{g}{R}}$, the bead will not be able to maintain any position $\theta >0$ on the hoop.

3.69

We know that $F_r=m(\ddot{r}-r{\dot{\theta }}^2)$ and ${F}_{\theta }=m(r\ddot{\theta }+2\dot{r}\dot{\theta })$. Balancing forces in the radial and tangential directions, we get

$$\begin{array}{rl}& F_{\theta }=m(r\ddot{\theta }+2\dot{r}\dot{\theta })=2m\dot{r}\dot{\theta }⟹\ddot{\theta }=0\\ & F_r=m(\ddot{r}-r{\dot{\theta }}^2)=0⟹\ddot{r}=r{\dot{\theta }}^2\end{array}$$

The first equation tells us that $\dot{\theta }$ is constant, and the second provides us with the differential equation we can use to solve for $r$ in terms of $\theta$.

$$\begin{array}{rl}\ddot{r}& =r{\dot{\theta }}^2\\ \dot{r}\frac{d\dot{r}}{dr}& =r{\dot{\theta }}^2\\ \int \dot{r}d\dot{r}& ={\dot{\theta }}^2\int rdr+c_1\\ {\dot{r}}^2& ={\dot{\theta }}^2{r}^2+2c_1\\ \int \frac{dr}{\sqrt{{\dot{\theta }}^2{r}^2+2c_1}}& =\int dt+c_2\end{array}$$

Let $C_1$ be $\sqrt{2c_1}$, and $\tan x$ be $\frac{\dot{\theta }r}{C_1}$. It follows that ${\sec }^{2}xdx=\frac{\dot{\theta }}{C_1}dr$.

$$\begin{array}{rl}\frac{1}{C_1}\int \frac{dr}{\sqrt{\frac{{\dot{\theta }}^2{r}^2}{C_1^2}+1}}=\frac{1}{\dot{\theta }}\int \frac{{\sec }^{2}xdx}{\sqrt{{\tan }^{2}x+1}}=\frac{1}{\dot{\theta }}\int \sec xdx& =\int dt+c_2\\ \frac{1}{\dot{\theta }}\ln (\sec x+\tan x)& =t+c_2\end{array}$$

Substituting the values of $\sec x$ and $\tan x$ in terms of $r$, we get

$$\begin{array}{rl}\frac{1}{\dot{\theta }}\ln \left(\sqrt{1+{\left(\frac{\dot{\theta }r}{C_1}\right)}^2}+\frac{\dot{\theta }r}{C_1}\right)& =t+c_2\\ \sqrt{1+{\left(\frac{\dot{\theta }r}{C_1}\right)}^2}& =e^{\dot{\theta }(t+c_2)}-\frac{\dot{\theta }r}{C_1}\\ 1+\cancel{{\left(\frac{\dot{\theta }r}{C_1}\right)}^2}& =e^{2\dot{\theta }(t+c_2)}+\cancel{{\left(\frac{\dot{\theta }r}{C_1}\right)}^2}-2e^{\dot{\theta }(t+c_2)}\frac{\dot{\theta }r}{C_1}\\ 2e^{\dot{\theta }(t+c_2)}\frac{\dot{\theta }r}{C_1}& =e^{2\dot{\theta }(t+c_2)}-1\\ r& =A^{\prime }{e}^{\dot{\theta }(t+c_2)}-B^{\prime }{e}^{-\dot{\theta }(t+c_2)}\end{array}$$

for some constants $A^{\prime }$ and $B^{\prime }$.

Let $\theta =\dot{\theta }t+{\theta }_0$, for some initial angle ${\theta }_0$. Now, the above equation can be rewritten as

$$\begin{array}{rl}r& =A^{\prime }{e}^{c_2\dot{\theta }-{\theta }_0}{e}^{\dot{\theta }t+{\theta }_0}-B^{\prime }{e}^{-c_2\dot{\theta }+{\theta }_0}{e}^{-(\dot{\theta }t+{\theta }_0)}\\ & =A{e}^{\theta }+B{e}^{-\theta }\end{array}$$

for some constants $A$ and $B$.