AlG1_L17

Eigenvectors and Eigenvalues

Definition 1(Definition).

An eigenvector $\mathbf{v}$ of a linear map $A$ is a nonzero vector such that $A\mathbf{v}=\lambda \mathbf{v}$ for some scalar $\lambda \in \mathbb{R}$.

Definition 2(Definition).

An eigenvalue of $A$ is a scalar $\lambda$ such that the equation $A\mathbf{v}=\lambda \mathbf{v}$ has a nontrivial solution.

If $A\mathbf{v}=\lambda \mathbf{v}$ for some nontrivial $\mathbf{v}$, then we say

1. $\mathbf{v}$ is an eigenvector for $\lambda$, and
2. $\lambda$ is an eigenvalue for $\mathbf{v}$.

Example 3(Example).

Let $A=\left[\begin{array}{cc}2& 2\\ -4& 8\end{array}\right]$. Consider the vectors $\mathbf{v}=\left[\begin{array}{c}1\\ 1\end{array}\right],\mathbf{w}=\left[\begin{array}{c}2\\ 1\end{array}\right]$.

Notice that $A\mathbf{v}=\left[\begin{array}{c}4\\ 4\end{array}\right]=4\mathbf{v}$. Thus $\mathbf{v}$ is an eigenvector of $A$.

On the other hand, $A\mathbf{w}=\left[\begin{array}{c}6\\ 0\end{array}\right]\ne \lambda \mathbf{w}$ for any $\lambda \in \mathbb{R}$. Thus $\mathbf{w}$ is not an eigenvector of $A$.

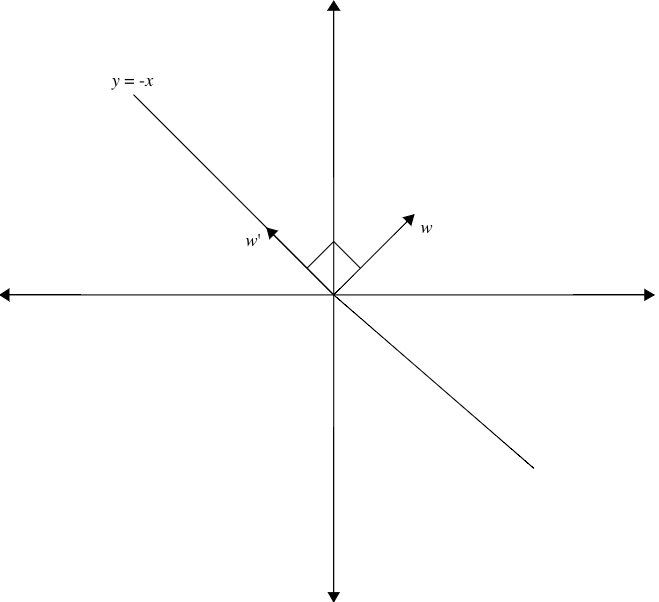
Example 4(Example: Reflection).

Let $T:{\mathbb{R}}^2\mapsto {\mathbb{R}}^2$ be the linear map that reflects over the line $L:y=-x$
Consider vectors $w$ and $w^{\prime }$, perpendicular to $L$ and parallel to $L$ respectively.
Notice that $w$ is an eigenvector with eigenvalue $-1$ and $w^{\prime }$ is an eigenvector with value $1$.

Example 5(Example: Projection).

Let $T:{\mathbb{R}}^2\mapsto {\mathbb{R}}^2$ be the projection map that projects a vector vertically onto the $x$-axis. Notice that the vectors lying on the x axis and y axis are eigenvectors with eigenvalues 1 and 0 respectively.

Example 6(Example: Rotation).

Consider a rotation map $R_{\theta }$ on ${\mathbb{R}}^2$ that rotates a vector by an angle $\theta \ne n\pi ,n\in \mathbb{Z}$.
In this case we can see geometrically that no eigenvectors exist.

Eigenvectors with distinct eigenvalues are linearly independent

Theorem 7(Theorem).

Let ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k$ be distinct eigenvalues of $A$, and ${\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_k$ be corresponding eigenvectors. Then, ${\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_k$ are linearly independent.

Proof
FTSOC, assume ${\mathbf{v}}_1,{\mathbf{v}}_2,...,{\mathbf{v}}_k$ are linearly dependent. Then, for some $j$, ${\mathbf{v}}_j$ is in the span of ${\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_{j-1}$. Choose smallest such $j$. This ensures ${\mathbf{v}}_1,{\mathbf{v}}_2,\dots ,{\mathbf{v}}_{j-1}$ are linearly independent. Since eigenvectors cannot be zero, $j>1$.

$$\begin{array}{rlr}{\mathbf{v}}_j& ={\alpha }_1{\mathbf{v}}_1+{\alpha }_2{\mathbf{v}}_2+\cdots +{\alpha }_{j-1}{\mathbf{v}}_{j-1}& (1)\\ {\lambda }_j{\mathbf{v}}_j& ={\alpha }_1{\lambda }_1{\mathbf{v}}_1+{\alpha }_2{\lambda }_2{\mathbf{v}}_2+\cdots +{\alpha }_{j-1}{\lambda }_{j-1}{\mathbf{v}}_{j-1},& (2)\end{array}$$

where $(2)$ is obtained by applying $A$ on $(1)$. ${\lambda }_j(1)-(2)$ yields:

$$\begin{array}{r}{\alpha }_1({\lambda }_j-{\lambda }_1){\mathbf{v}}_1+{\alpha }_2({\lambda }_j-{\lambda }_2){\mathbf{v}}_2+\cdots +{\alpha }_{j-1}({\lambda }_j-{\lambda }_{j-1}){\mathbf{v}}_{j-1}=0\end{array}$$

which is a nontrivial null linear combination of a set of linearly independent vectors. $\Rightarrow \Leftarrow$ ❏

Theorem 8(Corollary).

An $n\times n$ matrix has at most $n$ eigenvalues.

---

Eigenspaces

For a given real number $\lambda$ and a $n\times n$ matrix, how do you

1. check if $\lambda$ is an eigenvalue of $A$, and
2. if yes, find all eigenvectors corresponding to $\lambda$?

Eigenvectors with eigenvalue $\lambda$, if they exist, must satisfy

$$\begin{gathered} \begin{array}{rl}A\mathbf{v}& =\lambda \mathbf{v}\end{array} \\ ⟺(A-\lambda I)\mathbf{v}=0⟺\mathbf{v}\in \ker (A-\lambda I) \end{gathered}$$

This is great, since we already know how to find the kernel of a matrix.
If $\ker (A-\lambda I)=\{0\}$, then $\lambda$ is not an eigenvalue.

Definition 9(Definition:$\lambda -$eigenspace).

Let $A$ have eigenvalue $\lambda$. The $\lambda$-eigenspace of $A$ is the null space of $A-\lambda I$. Notice that since $\ker (A-\lambda I)$ is a subspace, the $\lambda -$eigenspace of an eigenvalue $\lambda$ is a subspace.

Example 10(Example).

Let $A=\left[\begin{array}{cc}2& -4\\ -1& -1\end{array}\right]$. We want to check if $\lambda =3$ is an eigenvalue.

$$\begin{array}{rl}A-3I& =\left[\begin{array}{cc}-1& -4\\ -1& -4\end{array}\right]\\ & \\ \text{RREF}(A-3I)& =\left[\begin{array}{cc}1& 4\\ 0& 0\end{array}\right]\end{array}$$

We can see that $\left[\begin{array}{c}-4\\ 1\end{array}\right]$ is the basis of the $3$-eigenspace of $A$.