ALG2_L3

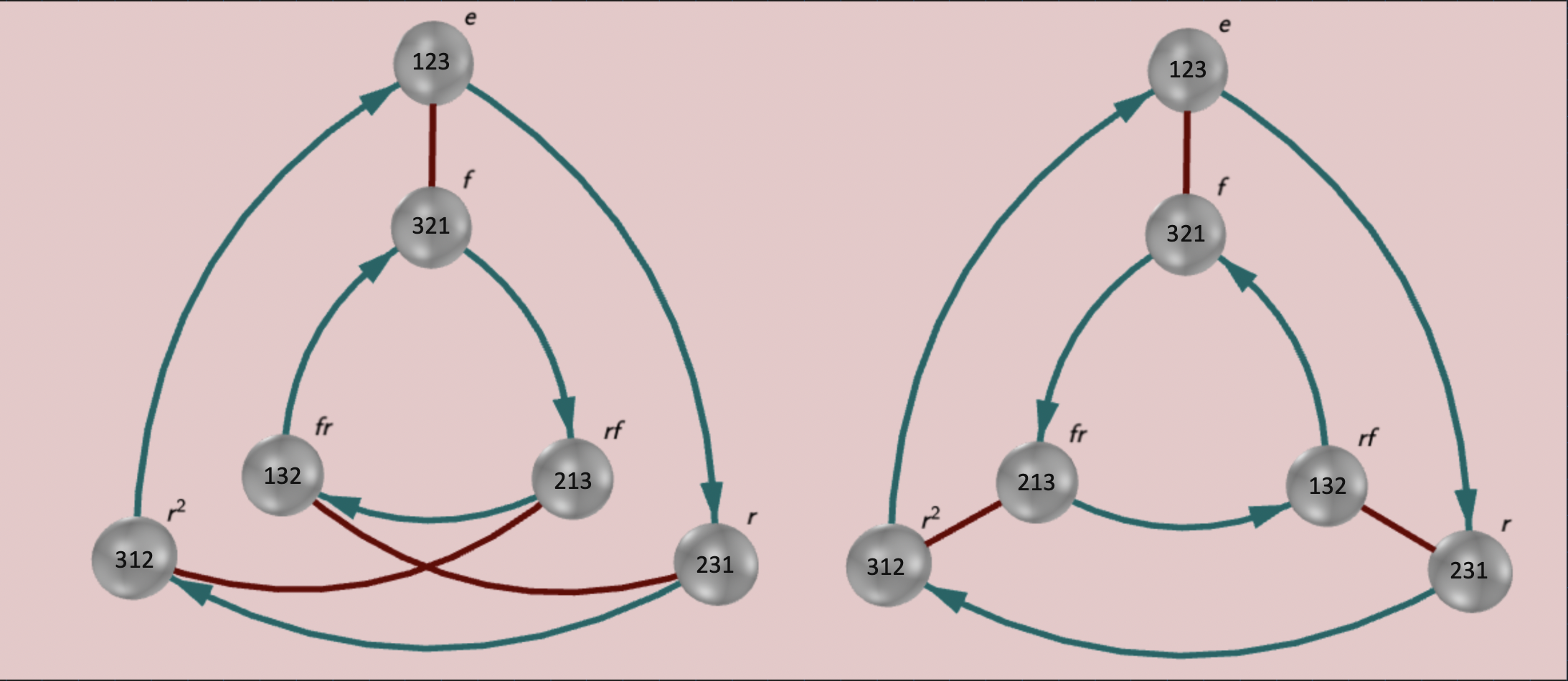
Cosets

Definition 1(Definition).

The right coset of $H$ is defined by $Hg\equiv \{hg:h\in H\}$, where $g\in G$.
The left coset of $H$ is defined by $gH\equiv \{gh:h\in H\}$ where $g\in G$.

Define two relations on $G$:

1. $a{\equiv }_{l}b\mathrm{mod}H$ if $b=ah$ for some $h\in H$, or equivalently, $a^{-1}b\in H$.
2. $a{\equiv }_{r}b\mathrm{mod}H$ if $b=ha$ for some $h\in H$, or equivalently, $b{a}^{-1}\in H$.

First, notice that these are equivalence relations. We will prove this assertion for ${\equiv }_r$.

Theorem 2(Proposition).

${\equiv }_r$ is an equivalence relation.

Proof
Reflexivity:
$g{\equiv }_{r}g\mathrm{mod}H$, since $e\in H$.

Symmetry:

$$\begin{array}{rl}& g{\equiv }_r{g}^{\prime }\mathrm{mod}H\\ ⟹& g{g}^{\prime -1}\in H\\ ⟹& (g{g}^{\prime -1}{)}^{-1}\in H\\ ⟹& g^{\prime }{g}^{-1}\in H\\ ⟹& g^{\prime }{\equiv }_{r}g\mathrm{mod}H\end{array}$$

Transitivity:
Let $g{\equiv }_r{g}^{\prime }\mathrm{mod}H$ and $g^{\prime }{\equiv }_r{g}^{\prime \prime }\mathrm{mod}H$. Then, $g{g}^{\prime -1}\in H$ and $g^{\prime }{g}^{\prime \prime -1}\in H$. It follows that $g{g}^{\prime -1}{g}^{\prime }{g}^{\prime \prime -1}=g{g}^{\prime \prime -1}\in H$, so $g{\equiv }_r{g}^{\prime \prime }\mathrm{mod}H$.

As we know, an equivalence relation on a set partitions the set into equivalence classes. We will now see that ${\equiv }_l$ partitions $G$ into its left cosets, and ${\equiv }_r$ partitions $G$ into its right cosets.

Theorem 3(Claim).

$Hg$ is the equivalence class $g$ under ${\equiv }_r$, i.e, $Hg=\{g^{\prime }:g{\equiv }_r{g}^{\prime }\mathrm{mod}H\}=[g]$.

Proof
$[g]\subset Hg$:
Let $g^{\prime }\in [g]$. Then, $g{g}^{\prime -1}=h$ for some $h\in H$. So, $h^{-1}g=g^{\prime }$.

$Hg\subset [g]$:
Let $hg\in Hg$. Obviously, $hg{g}^{-1}=h\in H$. Thus, $hg\in [g]$.

Important note

In a way, the algebraic representation and manipulation of group elements is detached from the objects whose symmetries the group may be modeling. For example, we can define the dihedral group $S_3$ algebraically like so: $⟨r,f:r^3=f^2=1,frf=r^{-1}⟩$. This definition tells us all we need to know about the group algebraically. However, when we try to associate the group elements generated by such an algebraic definition with configurations of the object whose symmetries the group describes, there are two way to do it, and they result in different Cayley diagrams. This is because (once we have associated a configuration to $r$ and $f$), we have to make sense of expressions like $rf$ as a configuration, and we can think of that as meaning either “first apply $r$, then $f$” or “first apply $f$, then $r$“. For non abelian groups, this will result in different configurations of the object being associated with $rf$. For example, if $f=(13)$ and $r=(132)$, $rf$ could be either $r(f(e))=r((13))=(12)$ or $f(r(e))=f((132))=(32)$, as illustrated below:

The usual convention to read $rf$ seems to be “first $r$, then $f$“. Regardless, this choice is pertinent only when we wish to associate the algebraic group elements with their configurational counterparts, and does not impact the algebra in any manner.

Lagrange’s theorem

Note that all left/right cosets of a subgroup $H$ of $G$ are of the same cardinality, since the maps $h\mapsto gh$ and $h\mapsto hg$ are bijective. This, combined with the fact that they partition $G$, gives us Lagrange’s theorem:

Theorem 4(Lagrange's Theorem).

Let $H<G$, where $G$ is finite. The order of $H$ divides $G$.

Theorem 5(Corollary).

The order of an element of a finite group divides the order of the group.

Theorem 6(Corollary).

Let $G$ be a finite group of prime order $p$. Let $a$ be any element of $G$ other than the identity. Then, $G$ is the cyclic group $⟨a⟩$ generated by $a$.

Theorem 7(Corollary).

Let $\varphi :G\to G^{\prime }$ be a homomorphism of finite groups. Then,

• $|G|=|\ker \varphi |\cdot |\mathrm{Im}\varphi |$
• $|\ker \varphi |$ divides $|G|$
• $|\mathrm{Im}\varphi |$ divides both $|G|$ and $|G^{\prime }|$.

Theorem 8(Corollary).

Let $K<H<G$ be subgroups of $G$. Then, $[G:K]=[G:H][H:K]$.

Example 9(A homomorphism$\varphi :S_4\to S_3$).

There are three ways to partition the set of four indices $\{1,2,3,4\}$ into pairs of subsets of order two, namely ${\Pi }_1:\{1,2\}\cup \{3,4\}$, ${\Pi }_2:\{1,3\}\cup \{2,4\}$, ${\Pi }_3:\{1,4\}\cup \{2,3\}$. An element of $S_4$ permutes the four indices, and by doing so it also permutes these partitions (no element of $S_4$ can map two different partitions to one, since the inverse of that element exists). Define $\varphi :S_4\to S_3$ by $\sigma \mapsto (\sigma ({\Pi }_1),\sigma ({\Pi }_2),\sigma ({\Pi }_3))$, where the latter is the permutation of $({\Pi }_1,{\Pi }_2,{\Pi }_3)$ made by $\sigma$, in non-cycle notation. What is the kernel of this homomorphism? Notice that the obvious elements that must be in the kernel are $e$, $(12)(34)$, $(13)(24)$, and $(14)(23)$. We can show that all other elements in $S_4$ are not in the kernel:

• Any $\sigma$ with only one 2-cycle will necessarily swap two elements in $({\Pi }_1,{\Pi }_2,{\Pi }_3)$.
• Any $\sigma$ with a 3-cycle can never map ${\Pi }_i$ to ${\Pi }_i$.
• Any $\sigma$ with a 4-cycle will necessarily swap two elements in $({\Pi }_1,{\Pi }_2,{\Pi }_3)$.

Thus, $\ker \varphi =\{e,(12)(34),(13)(24),(14)(23)\}$. Thus, the preimage of each ${\sigma }^{\prime }\in S_3$ is a coset $\sigma \ker \varphi$. To compute these is easy: for each ${\sigma }^{\prime }\in S_3$, first find one permutation $\sigma \in S_4$ such that $\varphi (\sigma )={\sigma }^{\prime }$. The rest of the preimage can be found by evaluating the coset $\sigma \ker \varphi$.

${\varphi }^{-1}({\Pi }_1,{\Pi }_2,{\Pi }_3)=\{e,(12)(34),(13)(24),(14)(23)\}$.
${\varphi }^{-1}({\Pi }_3,{\Pi }_1,{\Pi }_2)=\{(243),(142),(134),(123)\}$.
${\varphi }^{-1}({\Pi }_2,{\Pi }_3,{\Pi }_1)=\{(234),(124),(143),(132)\}$.
${\varphi }^{-1}({\Pi }_1,{\Pi }_3,{\Pi }_2)=\{(1324),(1423),(12),(34)\}$.
${\varphi }^{-1}({\Pi }_2,{\Pi }_1,{\Pi }_3)=\{(1243),(1342),(23),(14)\}$.
${\varphi }^{-1}({\Pi }_3,{\Pi }_2,{\Pi }_1)=\{(1234),(1432),(13),(24)\}$.

---

Quotient groups

Definition 10(Definition).

Let $H<G$. Then, $G/H$ is the set of equivalence classes of $G$ modulo $H$, i.e, $G/H=\{Hg:g\in G\}$. It can also be used to denote the set of all left cosets, $\{gH:g\in G\}$.

Normal subgroups

Definition 11(Definition).

A subgroup $N<G$ is called a normal subgroup if $gN{g}^{-1}=N$ for all $g\in G$. In other words, the left coset and right coset of $N$ for any given $g$ coincide. Denoted by $N◃G$.

Theorem 12(Lemma).

$N◃G$ $⟺$ the group operation $(g_{1}N)(g_{2}N)=g_1{g}_{2}N$ can be defined on $G/N$ where $g_1,g_2\in G$, $i$.$e$, $G/N$ is a group.

Proof of $⟹$
Let $N$ be a normal subgroup of $G$. It must be that $g_1{g}_{2}N$ does not depend on the choice of representatives $g_1$ and $g_2$ of each left coset, $g_{1}N$ and $g_{2}N$. To prove this, suppose $xN=g_{1}N$ and $yN=g_{2}N$ for some $x,y\in G$. Then,

$$\begin{array}{rl}& (xN)(yN)=xyN=x(g_{2}N)=\\ & x(N{g}_2)=(xN)g_2=(g_{1}N)g_2=\\ & g_1(N{g}_2)=g_1{g}_{2}N\end{array}$$

Proof of $⟸$
Let it be given that the operation $(g_{1}N)(g_{2}N)=g_1{g}_{2}N$ is well defined on $G/N$, i.e, for all $x,y,a,b\in G$ such that $xN=aN$ and $yN=bN$, we have $(ab)N=(xy)N$. Let $n\in N$ and $g\in G$. We have $gN=(eg)N=(eN)(gN)=(nN)(gN)=ngN$. Thus, $gN=ngN⟹N=g^{-1}ngN$, i.e, $g^{-1}ng\in N$, for all $n\in N$. It follows that $g^{-1}Ng=N$, or $Ng=gN$.

Theorem 13(Theorem).

A subgroup $N\le G$ is normal iff it is the kernel of some homomorphism.

Proof of $⟸$
Let $\varphi$ be a homomorphism between two groups $G$ and $H$. Let $n\in \ker \varphi$. Then, $\varphi (gn{g}^{-1})=\varphi (g)\varphi (n)\varphi (g^{-1})=\varphi (g)1_H\varphi (g^{-1})=\varphi (1_G)=1_H$. Thus, $gn{g}^{-1}\in \ker \varphi$. Also, $g{n}_1{g}^{-1}=g{n}_2{g}^{-1}⟹n_1=n_2$. Thus, $gN{g}^{-1}=N$.

Proof of $⟹$
Let $N⊴G$. Let $H=G/N$. Then, $N$ is the kernel of the projection map $a\mapsto aN$.

An immediate corollary of the above lemma is that the alternating group of $n$ elements $A_n$ is a normal subgroup of $S_n$, since $A_n$ is the kernel of the homomorphism $\varphi :S_n\to {\mathbb{Z}}_2$, $\varphi (\tau )=\text{sgn }\tau$.

Warning

The property “is a normal subgroup of” is not transitive. For example, $⟨s⟩◃⟨s,r^2⟩◃D_8$, but $⟨s⟩$ is not normal in $D_8$.

Cauchy’s Theorem

Theorem 14(Theorem).

If $G$ is a finite group and $p$ is a prime dividing $|G|$, then $G$ has an element of order $p$.

Proof
Define

$$\mathcal{S}=\left\{(x_1,\dots ,x_p)|x_i\in G,x_1{x}_2\dots x_p=1\right\}.$$

Note that $\mathcal{S}$ has $|G{|}^{p-1}$ elements (we are free to choose the first $p-1$ entries in the tuple, the last one must be the inverse of their product). Also note that any cyclic permutation of an element of $\mathcal{S}$ is also an element of $\mathcal{S}$:

$$\begin{array}{rl}& x_1{x}_2\dots x_p=1\\ ⟹& x_2\dots x_p=x_1^{-1}\\ ⟹& x_2\dots x_p{x}_1=1.\end{array}$$

Define the relation $\sim$ on $S$ by $\alpha \sim \beta$ if $\alpha$ is a cyclic permutation of $\beta$. Clearly, $\sim$ is an equivalence relation. Next, observe that every equivalence class in $S/\sim$ has order $1$ or $p$, since $p$ is prime. Moreover, equivalence classes of size $1$ are of the form $\{(x,x,\dots ,x)\}$ with $x^p=1$. Thus, $|G{|}^{p-1}=k+pd$, where $k$ is the number of equivalence classes of size $1$ and $d$ is the number of equivalence classes of size $p$. It follows that $p$ must divide $k$. Now, $\{(1,1,\dots ,1)\}$ is an equivalence class of size $1$. This forces the existence of a non-identity element of order $p$.